Find $$\begin{equation*} \displaystyle\iint\limits_{\kern-3ptR}(x+y)\sin (x-y)\,d\!A \end{equation*}$$

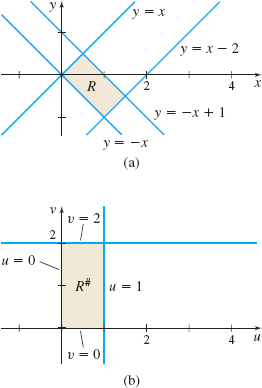
where $R$ is the region enclosed by $y=x$, $\ y=x-2$, $\ y=-x$, and $\ y=-x+1$.

Figure 64

Solution The integrand $(x+y)\sin (x-y)$ suggests changing the variables to $u=x+y$ and $v=x-y$. Then the lines $x-y=0$, $\ x-y=2$, $\ x+y=0$, and $\ x+y=1$ in the $xy$-plane define the region $R$, and the lines $v=0,$ $v=2,$ $u=0,$ and $u=1$ in the $uv$-plane define the region $R^{\#}$. See Figure 64. We solve the system of equations $\left\{ \begin{array}{l} u=x+y \\[3pt] v=x-y \end{array} \right.$ for $x$ and $y$, and obtain $$\begin{equation*} x=\dfrac{u+v}{2}\qquad y=\dfrac{u-v}{2} \end{equation*}$$

Using these equations, the Jacobian is $$\begin{equation*} \dfrac{\partial (x,y)}{\partial (u,v)}=\left\vert \begin{array}{l@{\quad}r} \dfrac{1}{2} & \dfrac{1}{2} \\[9pt] \dfrac{1}{2} & -\dfrac{1}{2} \end{array} \right\vert =-\dfrac{1}{4}-\dfrac{1}{4}=-\dfrac{1}{2} \end{equation*}$$

The integral under this change of variables becomes $$\begin{eqnarray*} \iint\limits_{\kern-3ptR}(x+y)\sin (x-y)\,d\!A& =&\iint\limits_{\kern-3ptR^{\#}}u\sin v\cdot \left\vert -\dfrac{1}{2}\right\vert \,du\,dv=\dfrac{1}{2}\int_{0}^{1} \int_{0}^{2}u\sin v\,dv\,du \notag \\ & =&\dfrac{1}{2}\int_{0}^{1}\big[u(-\cos v)\big] _{0}^{2}\,du= \dfrac{1}{2}(1-\cos 2)\int_{0}^{1}u\,du \notag \\[4.5pt] & =&\dfrac{1}{4}(1-\cos 2) \end{eqnarray*}$$