Use Fubini’s Theorem for an \(x\)-Simple Region

Find \(\iint\limits_{\kern-3ptR} xy\,dA\) if \(R\) is the region enclosed by \(y=x^{2}\) and \(y=\sqrt{x}.\)

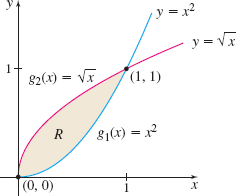
Solution We begin by graphing the region \(R.\) See Figure 13. Observe that \(R\) is a closed, bounded region. Also notice that the bottom and top boundaries of \(R\) are smooth curves expressed as functions of \(x\): \(g_{1}(x) =x^{2}\), \(g_{2}(x)=\sqrt{x}\), \(0\leq x\leq 1\). That is, \(R\) is \(x\)-simple, so we can use Fubini’s Theorem. \begin{eqnarray*} \displaystyle\iint\limits_{\kern-3ptR} xy\,{\it dA} &=&\int_{0}^{1}\left[ \int_{x^{2}}^{\sqrt{x}}xy\,{\it dy} \right] \! {\it dx}=\int_{0}^{1}x \left[ \dfrac{y^{2}}{2}\right] _{x^{2}}^{ \sqrt{x}}{\it dx}\\[4pt] &=&\int_{0}^{1}x\!\left(\dfrac{x-x^{4}}{2}\right)\!{\it dx}=\dfrac{1}{2} \int_{0}^{1}(x^{2}-x^{5})\,{\it dx}\\[4pt] &=&\dfrac{1}{2}\left[ \dfrac{x^{3}}{3}-\dfrac{x^{6}}{6}\right] _{0}^{1}=\dfrac{1 }{12} \end{eqnarray*}