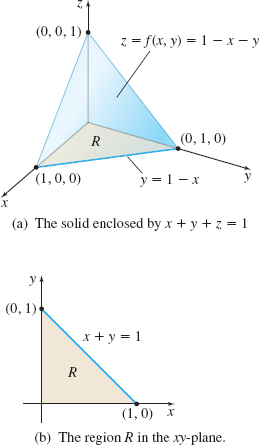
Using a Double Integral to Find the Volume of a Solid

Find the volume \(V\) of the solid in the first octant enclosed by the plane \(x+y+z=1\).

Solution Figure 21(a) shows the solid in the first octant enclosed by the plane \(x+y+z=1\). The volume \(V\) of the solid lies under the plane \(z=f(x,y) =1-x-y\) and above the region \(R\) in the \(xy\)-plane bounded by the lines \(x=0,\) \(y=0,\) and \(x+y=1.\) See Figure 21(b). The region \(R\) is \(x\)-simple and \(y\)-simple. If we treat \(R\) as \(x\)-simple, then \(y\) varies from \(y=0\) to \(y=1-x\), \(0\leq x \leq 1\). The volume \(V\) of the solid is \begin{eqnarray*} V=\displaystyle\iint\limits_{\kern-3ptR}f(x,y) \,{\it dA}& =&\int_{0}^{1}\left[ \int_{0}^{1-x}(1-x-y)\,{\it dy}\right]\! {\it dx}=\int_{0}^{1}\left[ ( 1-x) y- \dfrac{y^{2}}{2}\right] _{0}^{1-x} {\it dx}\\[5pt] &=&\int_{0}^{1}\left[ (1-x)^{2}-\dfrac{(1-x)^{2}}{2}\right] \! {\it dx} \\[5pt] & =&\dfrac{1}{2}\int_{0}^{1}(1-x)^{2}\,{\it dx}=\dfrac{1}{2}\left[ x-x^{2}+\dfrac{x^{3} }{3}\right] _{0}^{1}=\dfrac{1}{6}\hbox{ cubic unit} \end{eqnarray*}