Finding a Double Integral Using Polar Coordinates

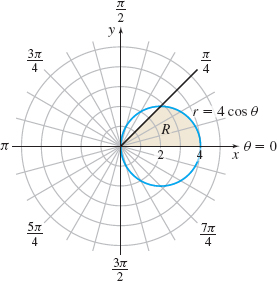
Find \(\displaystyle\iint\limits_{\kern-3ptR}\cos \theta \,{\it dA}\), where \(R\) is the region enclosed by the rays \(\theta =0\) and \(\theta =\dfrac{\pi }{4}\) and the circle \(r=4\cos \theta\).

Solution We begin with a graph of the region \(R\). See Figure 26. Notice that \(\theta\) varies from \(0\) to \(\dfrac{\pi }{4}\) and \(r\) varies from \(r_{1}=0\) to the circle \(r_{2}=4\cos \theta\). Then \[ \begin{array} \displaystyle\iint\limits_{\kern-3ptR}\cos \theta \,{\it dA} &=&\int_{0}^{\pi /4}\int_{0}^{4\cos \theta }r\cos \theta \,dr\,d\theta =\int_{0}^{\pi /4}\left[ \dfrac{r^{2}}{2}\cos \theta \right] _{0}^{4\cos \theta }d\theta =\int_{0}^{\pi /4}8\cos ^{3}\theta \,d\theta \notag \\[4pt] &=&8\int_{0}^{\pi /4}(1-\sin ^{2}\theta )\cos \theta \,d\theta = 8\int_{0}^{\sqrt{2}/2}(1-u^{2})\, du\\[-8pt] && \qquad \qquad \qquad \quad \underset{\color{#0066A7}{\hbox{\(u=\sin \theta ;\, {du}=\cos \theta\, d\theta\)}}}{\color{#0066A7}{\uparrow }}\\[8pt] &=&8\left[ u-\dfrac{u^{3}}{3}\right] _{0}^{\sqrt{2}/2}=8\left[ \dfrac{\sqrt{2} }{2}-\dfrac{\sqrt{2}}{12}\right] =\dfrac{10\sqrt{2}}{3} \end{array} \]