Finding the Mass and the Center of Mass of a Lamina

Find the mass \(M\) and the center of mass \((\bar{x},\bar{y})\) of a lamina in the shape of a region \(R\) in the \(xy\)-plane that lies outside the circle \( x^{2}+y^{2}=a^{2}\) and inside the circle \(x^{2}+y^{2}=2ax.\) The mass density \(\rho \) is inversely proportional to the distance from the origin.

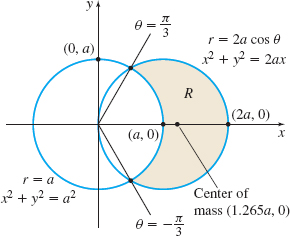
Solution Figure 34 illustrates the region \(R\). Since \(R\) involves two circles, we use polar coordinates. Then the two circles are given by \( r=a \) and by \(r=2a\cos \theta \). The circles intersect when \(a=2a\cos \theta \) or \(\cos \theta =\dfrac{1}{2},\) and the points of intersection are \(\left( a,\dfrac{\pi }{3}\right) \) and \(\left( a,-\dfrac{\pi }{3}\right) .\) The region \(R\) is given by \(a\leq r\leq 2a\cos \theta ,\) \(-\dfrac{\pi }{3}\leq \theta \leq \dfrac{\pi }{3}.\)

Since the distance of a point \((x,y)\) from the origin is \(\sqrt{x^{2}+y^{2}}\) , the mass density of the lamina at any point \((x,y)\) in \(R\) is \[ \rho (x,y)=\dfrac{k}{\sqrt{x^{2}+y^{2}}}=\dfrac{k}{r} \qquad {\color{#0066A7}{\hbox{\(r^{2} =x^{2} + y^{2}\)}}} \]

where \(k\) is the constant of proportionality. Since \(R\) does not contain the origin, the mass density \(\rho =\rho (x,y)\) is continuous on \(R.\) The mass \(M\) of the lamina is \[ \begin{eqnarray*} M &=&\displaystyle\iint\limits_{\kern-3ptR}\rho (x,y)\,{\it dA}=k\displaystyle\iint\limits_{\kern-3ptR}\dfrac{rdr\,d\theta }{r} =k\int_{-\pi /3}^{\pi /3}\int_{a}^{2a\cos \theta }\,dr\,d\theta \\[4pt] &=&k \int_{-\pi /3}^{\pi /3}(2a\cos \theta -a)\,d\theta =k\big[2a\sin \theta -a\theta \big] _{-\pi /3}^{\pi /3}= k\!\left( 2a\sqrt{3}-a\dfrac{2\pi }{3}\right)\\[4pt] &=&\dfrac{2ka}{3}(3\sqrt{3}-\pi ) \end{eqnarray*} \]

Both the mass density function and the region \(R\) are symmetric about the \(x\)-axis. So, the center of mass lies on the \(x\)-axis; that is, \(\bar{y}=0\). To find \(\bar{x}\), we first find \(M_{y}\). \[ \begin{eqnarray*} M_{y}& =&\displaystyle\iint\limits_{\kern-3ptR}x\rho (x,y)\,{\it dA}=\displaystyle\iint\limits_{\kern-3ptR}( r\cos \theta ) \left( \dfrac{k}{r}\right) r\,dr\,d\theta =k\int_{-\pi /3}^{\pi /3}\int_{a}^{2a\cos \theta }r\cos \theta \,dr\,d\theta\\[4pt] &=&\dfrac{k}{2}\int_{-\pi /3}^{\pi /3}(4a^{2}\cos ^{2}\theta -a^{2})\cos \theta \,d\theta = a^{2}\dfrac{k}{2}\int_{-\pi /3}^{\pi /3}(3-4\sin ^{2}\theta )\cos \theta \,d\theta\\[4pt] &=&\dfrac{a^{2}k}{2}\left[ 3\sin \theta -\dfrac{4\sin ^{3}\theta }{3} \right] _{-\pi /3}^{\pi /3}=ka^{2}\sqrt{3} \end{eqnarray*} \]

Then \[ \bar{x}=\dfrac{M_{y}}{M}=\dfrac{ka^{2}\sqrt{3}}{\dfrac{2ka}{3}(3\sqrt{3}-\pi )} =\dfrac{3a\sqrt{3}}{2(3\sqrt{3}-\pi )}\approx 1.265a \]

The center of mass is approximately \((1.265a,0)\).