Finding a Line Integral Using Green’s Theorem

Use Green’s Theorem to find the line integral \[ \begin{equation*} \oint_{C}[ ( -2xy+y^{2}) \,dx+x^{2}\,dy] \end{equation*} \]

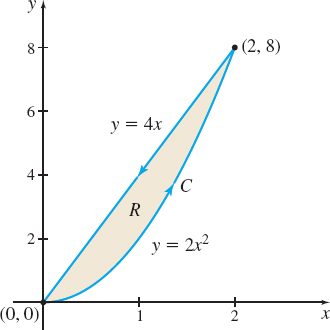
where \(C\) is the boundary of the region \(R\) enclosed by \(y=4x\) and \(y=2x^{2}\).

Solution Figure 33 illustrates the curve \(C\) and the region \(R\). \(C\) is a piecewise-smooth closed curve and \(R\) is both simply connected and closed. We let \[ \begin{equation*} P(x,y)=-2xy+y^{2}\qquad \hbox{and}\qquad Q(x,y)=x^{2} \end{equation*} \]

Since \(P\) and \(Q\) have continuous first-order partial derivatives in \(R,\) we use Green’s Theorem. Then \[ \begin{eqnarray*} \oint_{C}(P\,dx+Q\,dy)& =&\iint\limits_{R}\left( \dfrac{\partial Q}{\partial x }-\dfrac{\partial P}{\partial y}\right) \,dx\,dy \\ \oint_{C}[(-2xy+y^{2})\,dx+x^{2}\,dy]& =&\iint\limits_{R}\left[ \dfrac{ \partial }{\partial x}(x^{2})-\dfrac{\partial }{\partial y}(-2xy+y^{2})\right] \,dx\,dy\\ &=&\iint\limits_{R}(4x-2y)\,dx\,dy \underset{\underset{\color{#0066A7}{R\hbox{ is } x\hbox{-simple}}}{\color{#0066A7}{\uparrow}}} {=} \int_{0}^{2} \int_{2x^{2}}^{4x}(4x-2y)\,dy\,dx \\ & =&\int_{0}^{2}\big[ 4xy-y^{2}\big] _{2x^{2}}^{4x}\,dx = \int_{0}^{2}[(16x^{2}-16x^{2})-(8x^{3}-4x^{4})]\,dx \\ & =&\left[ -2x^{4}+\dfrac{4}{5}x^{5}\right] _{0}^{2}=-32+\dfrac{128}{5}=\dfrac{ -32}{5} \end{eqnarray*} \]