Using Green’s Theorem to Find a Line Integral

Find \(\oint_{\!\!\!\!C}\left( \dfrac{-y}{x^{2}+y^{2}}\,dx+\dfrac{x}{x^{2}+y^{2}} \,dy\right) \) if:

1. \(C\) is the curve \(x^{2/3}+y^{2/3}=1,\) whose orientation is counterclockwise.
2. \(C\) is any piecewise-smooth, simple closed curve not containing the origin in its interior.

1013

Solution For \(P=\dfrac{-y}{x^{2}+y^{2}}\) and \( Q=\dfrac{x}{ x^{2}+y^{2}}\), we have \[ \dfrac{\partial P}{\partial y}=\dfrac{y^{2}-x^{2}}{(x^{2}+y^{2})^{2}}\qquad \hbox{and} \qquad \dfrac{\partial Q}{\partial x}=\dfrac{y^{2}-x^{2}}{(x^{2}+y^{2})^{2}} \]

Notice that, except at the point \((0,0),\) the partial derivatives \(\dfrac{ \partial P}{\partial y}\) and \(\dfrac{\partial Q}{\partial x}\) are continuous.

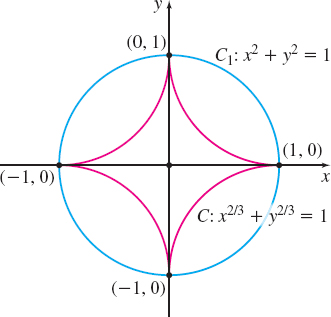
(a) It is difficult to find the line integral along \(C\). Moreover, because \(x^{2/3}+y^{2/3}=1\) contains the point \((0,0)\) in its interior, we cannot use Green’s Theorem as we did in Example 2 to change the line integral to a double integral. However, since \(\dfrac{ \partial P}{\partial y}=\dfrac{\partial Q}{\partial x}\) throughout \(R,\) we can use a different curve that leads to an easier line integral. For example, suppose we replace \(x^{2/3}+y^{2/3}=1\) by the unit circle \(C_{1}\): \(x^{2}+y^{2}=1,\) noting that the conditions required for \(\int_{C}( P\,dx+Q\,dy)\) to equal \(\int_{C_{1}}( P\,dx+Q\,dy)\) are met. See Figure 38.

On \(C_{1},\) \(x=\cos \theta\), \(y=\sin \theta\), \(0\leq \theta \leq 2\pi\). Then \(dx=-\sin \theta d\theta \), \(dy=\cos \theta d\theta\), and \[ \begin{eqnarray*} \oint_{C}\left( \dfrac{-y}{x^{2}+y^{2}}\,dx+\dfrac{x}{x^{2}+y^{2}}\,dy\right) &=&\oint_{C_{1}}\left( \dfrac{-y}{x^{2}+y^{2}}\,dx+\dfrac{x}{x^{2}+y^{2}} \,dy\right)\\ &=&\int_{0}^{2\pi }(\sin ^{2}\theta +\cos ^{2}\theta )\,d\theta =2\pi \end{eqnarray*} \]

(b) In this case, the interior of the curve \(C\) does not contain the origin. Since \[ \begin{equation*} \dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x} \end{equation*} \]

in the simply connected region \(R\) enclosed by \(C\), it follows that \(\mathbf{ F}=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j}\) is a conservative vector field. Since \(C\) is closed, \[ \oint_{C}\left( \dfrac{-y}{x^{2}+y^{2}}\,dx+\dfrac{x}{x^{2}+y^{2}}\,dy\right)= \oint_{C}\mathbf{F}\,{\bf\cdot}\, d\mathbf{r} =0 \]