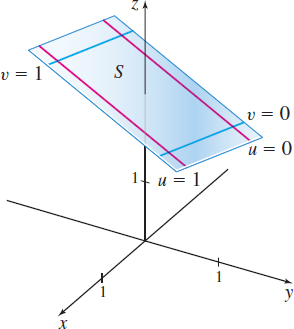
Describing a Parametric Surface
- Describe the parametric surface \(S\) given by \(\mathbf{r}(u,v) =( 1+2u+v) \mathbf{i}+(u-v) \mathbf{j} +(3+v) \mathbf{k}\).
- Find a rectangular equation for \(S.\)
Solution (a) We begin by finding several coordinate curves. We choose to use \(v=0,\) \(v=1,\) \(u=0,\) and \(u=1,\) but any numbers will do.
When \(v=0,\) the \(u\)-coordinate curve is \(\mathbf{r} ( u,0) = (1+2u) \mathbf{i}+u\mathbf{j}+3\mathbf{k}\).
When \(v=1,\) the \(u\)-coordinate curve is \(\mathbf{r} ( u,1) = (2+2u) \mathbf{i}+ ( u-1) \mathbf{j}+4\mathbf{k}\).
When \(u=0,\) the \(v\)-coordinate curve is \(\mathbf{r} ( 0,v) = ( 1+v) \mathbf{i}-v\mathbf{j}+(3+v) \mathbf{k}\).
When \(u=1,\) the \(v\)-coordinate curve is \(\mathbf{r} ( 1,v) =(3+v) \mathbf{i}+ ( 1-v) \mathbf{j}+(3+v) \mathbf{k}\).
The graph of the parametric surface is a plane as shown in Figure 41.
(b) To find a rectangular equation for the surface, we write the components of \(\mathbf{r=r}(u,v) \) as a system of equations. Since \(\mathbf{r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}=x(u,v) \mathbf{i}+y(u,v) \mathbf{j}+z(u,v) \mathbf{k},\) we have\[ \left\{ \begin{array}{ll@{\qquad}l} x=2u+v+1 & &{\color{#0066A7}{(1)}}\\ y=u-v & & {\color{#0066A7}{(2)}}\\ z= v+3 & & {\color{#0066A7}{(3)}} \end{array} \right. \]
If we eliminate \(u\) and \(v\) from this system, we will have an expression involving \(x,\) \(y,\) and \(z.\) We eliminate \(v\) by adding equations \((1) \) and \((2) \) and equations \((2) \) and \((3) .\) \[ \begin{equation*} \begin{array}{ll@{\qquad\qquad}l} x+y=3u+1 & & \color{#0066A7}{{\hbox{(4) Add \(1\) and \(2\).}}}\\ y+z= \hspace{6pt}u+3 & &\color{#0066A7}{{\hbox{(5) Add \(2\) and \(3\).}}} \end{array} \end{equation*} \]
Now we eliminate \(u\): \[ \begin{equation*} \begin{array}{ll@{\qquad}l} \hspace{48pt}x+ y = 3u+1 & & \color{#0066A7}{(4)} \\[5pt] \hspace{27pt}\underline{\,\ -3y-3z=-3u-9} & \,\ \ \ \ \ \ \ \ \ \ & \color{#0066A7}{{\hbox{Multiply (5) by \(-3\).}}} \\ \hspace{21pt}x-2y-3z=-8 & & \color{#0066A7}{{\hbox{Add.}}} \end{array} \end{equation*} \]
This is the equation of a plane whose normal vector is \(\mathbf{i}-2\mathbf{j}-3\mathbf{k}.\)