EXAMPLE 3Representing a Surface Parametrically
Find a parametrization of the surface S given by x+y2+z=50≤x≤1−1≤y≤1
Solution We begin by expressing S as an explicit function of x and y. z=f(x,y)=5−x−y2
Since z is a function of x and y, we let x=u and y=v. Then the parametric equations of S are x=uy=vz=5−u−v2
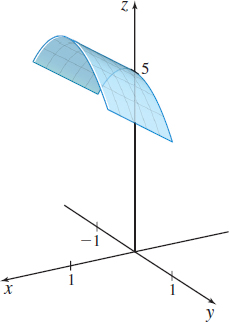
Figure 43 r(u,v)=ui+vj+(5−u−v2)k,0≤u≤1,−1≤v≤1
Using these parametric equations, we obtain r(u,v)=ui+vj+(5−u−v2)k0≤u≤1−1≤v≤1