Parametrizing a Cone Using Different Coordinate Systems

Find a parametrization of the surface \(S\) defined by the cone \[ z=\sqrt{3x^{2}+3y^{2}}\qquad x^{2}+y^{2}\leq 16 \]

1. Using rectangular coordinates.
2. Using cylindrical coordinates.
3. Using spherical coordinates.

Solution (a) The equation is given in rectangular coordinates and is written explicitly as a function \(z=f(x,y) .\) So, we define \(x=u,\) \(y=v,\) \(z=\sqrt{3u^{2}+3v^{2}}.\) Then a parametrization of the cone is \[ \mathbf{r}(u,v) =u\mathbf{i}+v\mathbf{j}+\sqrt{3u^{2}+3v^{2}}\, \mathbf{k}\qquad u^{2}+v^{2}\leq 16 \]

(b) In cylindrical coordinates, the cone is given by \[ z=\sqrt{3x^{2}+3y^{2}}=\sqrt{3}\sqrt{( r\cos \theta ) ^{2}+(r\sin \theta ) ^{2}}=\sqrt{3}\sqrt{r^{2}}=\sqrt{3}\,r \]

where \(z\) is expressed explicitly in terms of \(r\) and \(\theta .\) So if we use \(r\) and \(\theta \) as parameters, then a parametrization of the cone is \[ \begin{eqnarray*} \mathbf{r}( r,\theta ) =r\cos \theta \,\mathbf{i}+ \underset{\underset{\color{#0066A7}{x=r\cos \theta ,y= r\sin \theta , z=\sqrt{3}r}}{\color{#0066A7}{\uparrow}}}{r\sin \theta \, \mathbf{j}}+\sqrt{3}r\,\mathbf{k}\qquad 0\leq r\leq 4\quad 0\leq \theta \leq 2\pi \end{eqnarray*} \]

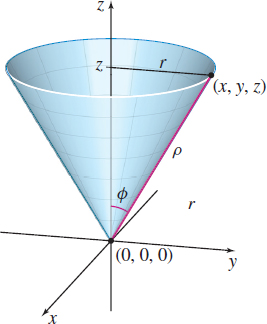
(c) In spherical coordinates, the equation of a half cone, where \(z\geq 0,\) is \(\phi =a,\) \(0< a <\dfrac{\pi }{2}.\) We use Figure 45 to find \(a.\) \[ \begin{eqnarray*} \tan \phi &=&\dfrac{r}{z}=\dfrac{r}{\sqrt{3}r}=\dfrac{1}{\sqrt{3}}\qquad \color{#0066A7}{{\hbox{\(z=\sqrt{3}r\)}}}\\[6pt] \phi &=&\tan ^{-1}\dfrac{1}{\sqrt{3}}=\dfrac{\pi }{6}=a \end{eqnarray*} \]

Using \(\rho \) and \(\theta \) as parameters, parametric equations for the cone in spherical coordinates are \[ \begin{eqnarray*} x\underset{\underset{\color{#0066A7}{\sin \tfrac{\pi }{6}=\tfrac{1}{2}}}{\color{#0066A7}{\uparrow }}}{=}\dfrac{ \rho }{2}\cos \theta \qquad y\underset{\underset{\color{#0066A7}{\sin \tfrac{\pi }{6}=\tfrac{1}{2}}}{\color{#0066A7}{\uparrow }}}{=}\dfrac{\rho }{2}\sin \theta \qquad z \underset{\underset{\color{#0066A7}{\cos \tfrac{\pi }{6}=\tfrac{\sqrt{3}}{2}}}{\color{#0066A7}{\uparrow }}}{=}\dfrac{\sqrt{3}}{2}\rho \end{eqnarray*} \]

Now we find the parameter domain. Since \[ z^{2}=3x^{2}+3y^{2} \ \hbox{and}\ \rho ^{2}=x^{2}+y^{2}+z^{2}=x^{2}+y^{2}+ (\underset{\color{#0066A7}{z^{2}}}{\underbrace{ 3x^{2}+3y^{2}}})=4x^{2}+4y^{2} \]

we have \[ 0\leq \rho ^{2}=4(x^{2}+y^{2}) \leq 4\,{\cdot}\, 16=64,\ \hbox{or equivalently,}\ 0\leq \rho \leq 8.\]

The parameter domain of the cone is \(0\leq \rho \,\leq 8\) and \(0\leq \theta \leq 2\pi .\) Then a parametrization of the cone is \[ \mathbf{r}( \rho ,\theta ) =\dfrac{\rho }{2}\cos \theta \,\mathbf{ i}+\dfrac{\rho }{2}\sin \theta \,\mathbf{j}+\dfrac{\sqrt{3}}{2}\rho \, \mathbf{k}\qquad 0\leq \rho \leq 8\quad 0\leq \theta \leq 2\pi \]