Find Equations for a Tangent Plane and a Normal Line

1. Find an equation of the tangent plane to the surface \(S\) parametrized by \(\mathbf{r=r}(u,v) =3u\mathbf{i}+( 6-u^{2}-v^{2}) \mathbf{j}+2v \mathbf{k\ }\) at the point \(( -3,1,4) .\)
2. Find an equation of the normal line to the tangent plane at \((-3,1,4) .\)

Solution (1) We begin by finding the values of the parameters at the point \(( -3,1,4) .\) That is, we solve the system of equations \[ \left\{ \begin{array}{rcl@{\qquad}r} 3u &=&-3 & \color{#0066A7}{{\hbox{\((1)\)}}}\\ 6-u^{2}-v^{2}&=& 1 & \color{#0066A7}{{\hbox{\((2)\)}}}\\ 2v&=& 4 & \color{#0066A7}{{\hbox{\((3)\)}}} \end{array} \right. \]

From \(( 1) \) we find \(u=-1,\) and from (3) we find \(v=2.\) [Checking, we find these values also satisfy (2).]

We now find the tangent vectors \(\mathbf{r}_{u}\) and \(\mathbf{r}_{v}.\) \[ \begin{array}{@{\hspace*{-2.2pc}}rcl@{\qquad}lrll} \mathbf{r}_{u} &=&\dfrac{\partial }{\partial u}( 3u) \mathbf{i}+ \dfrac{\partial }{\partial u}( 6-u^{2}-v^{2}) \mathbf{j}+\dfrac{ \partial }{\partial u}\left( 2v\right) \mathbf{k}=3\mathbf{i}-2u\,\mathbf{j} & \mathbf{r}_{u}( -1,2) &=&3\mathbf{i}+2\,\mathbf{j}\\[4pt] \mathbf{r}_{v} &=&\dfrac{\partial }{\partial v}( 3u) \mathbf{i}+ \dfrac{\partial }{\partial v}( 6-u^{2}-v^{2}) \mathbf{j}+\dfrac{ \partial }{\partial v}( 2v) \mathbf{k}=-2v\mathbf{j}+2\,\mathbf{k} & \mathbf{r}_{v}( -1,2) &=&-4\mathbf{j}+2\, \mathbf{k} \end{array} \]

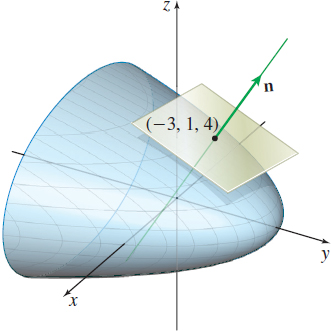
The normal vector \(\mathbf{n}\) to the tangent plane at \(( -3,1,4) \) is \[ \mathbf{n} = \mathbf{r}_u ( -1,2) \times \mathbf{r}_v ( -1,2) =\left\vert \begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] 3 & 2 & 0 \\[3pt] 0 & -4 & 2 \end{array} \right\vert =4\mathbf{i}-6\mathbf{j}-12\mathbf{k} \]

An equation of the tangent plane is \[ 4( x+3) -6( y-1) -12( z-4) =0\qquad\hbox{or equivalently}\qquad 4x-6y-12z=-66 \]

(b) The normal line to the tangent plane contains the point \(( -3,1,4) \) and is parallel to the vector \(\mathbf{n}=4\mathbf{i}-6\mathbf{j} -12\mathbf{k}\). A parametrization of the normal line is \[ \mathbf{r}(t) = ( -3+4t ) \mathbf{i}+ ( 1-6t ) \mathbf{j} + ( 4-12t ) \mathbf{k} \]

See Figure 48.