Finding a Tangent Plane and a Normal Line

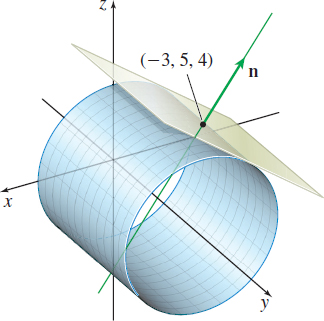
A surface \(S\) is defined by \(x^{2}+z^{2}=25\) and \(0\leq y\leq 10.\)

1. Find a smooth parametrization for \(S.\)
2. Find an equation of the tangent plane to \(S\) at the point \(( -3,5,4) .\)
3. Find an equation of the normal line to the tangent plane at \((-3,5,4) .\)

Solution (a) Since \(S\) is a circular cylinder, we choose a parametrization that uses a variation of cylindrical coordinates. If \(x=r\cos \theta ,\) \(y=y,\) and \(z=r\sin \theta ,\) then \(x^{2}+z^{2}=r^{2}=25,\) or equivalently, \(r=5\). Then parametric equations for the cylinder are \[ x=5\cos \theta \qquad y=y\qquad z=5\sin \theta \]

and a parametrization of \(S\) is \[ \begin{equation*} \mathbf{r}( \theta ,y) =5\cos \theta\ \mathbf{i}+y\mathbf{j}+5\sin \theta\ \mathbf{k} \end{equation*} \]

where the parameter domain is \(0\leq \theta \leq 2\pi \) and \(0\leq y\leq 10.\)

1023

To determine whether this is a smooth parametrization, we find the partial derivatives of \(\mathbf{r=\mathbf{r}}( \theta ,y)\). \[ \mathbf{r}_{\theta }( \theta ,y) =-5\sin \theta\ \mathbf{i}+5\cos \theta\ \mathbf{k}\qquad \mathbf{r}_{y}( \theta ,y) =\mathbf{j} \]

Each of these is continuous. Now \[ \mathbf{r}_{\theta }\times \mathbf{r}_{y}= \left|\begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ -5\sin \theta & 0 & 5\cos \theta \\ 0 & 1 & 0 \end{array}\right| =-5\cos \theta\ \mathbf{i}-5\sin \theta\ \mathbf{k} \]

Since \(\left\Vert \mathbf{r}_{\theta }\times \mathbf{r}_{y}\right\Vert =\left\Vert -5\cos \theta\ \mathbf{i}-5\sin \theta\ \mathbf{k}\right\Vert =\sqrt{25\cos ^{2}\theta +25\sin ^{2}\theta }=5,\) then \(\mathbf{r}_{\theta }\times \mathbf{r}_{y}\neq \mathbf{0}\). So, \(\mathbf{r}=\mathbf{r}( \theta ,y) \mathbf{\ }\) is a smooth parametrization, and \(S\) is a smooth surface.

(b) At the point \(( -3,5,4) ,\) we have \(5\cos \theta =-3,\) \(y=5,\) and \(5\sin \theta =4.\) Then the normal vector \(\mathbf{n}\) to the plane at \(( -3,5,4) \) is \(\mathbf{r}_{\theta }\times \mathbf{r} _{y}=-5\left( -\dfrac{3}{5}\right) \mathbf{i}-5\left( \dfrac{4}{5}\right) \mathbf{k}=3\mathbf{i}-4\mathbf{k}.\) An equation of the tangent plane is \[ 3( x+3) -4( z-4) =0\qquad \hbox{or equivalently}\qquad 3x-4z=-25 \]

(c) The normal line to the tangent plane contains the point \(( -3,5,4) \) and is parallel to \(3\mathbf{i}-4\mathbf{k}\). A parametrization of the normal line is \(\ \mathbf{r}(t) =(-3+3t) \mathbf{i}+5\mathbf{j}+( 4-4t) \mathbf{k}\). See Figure 49.