Finding the Centroid of a Surface

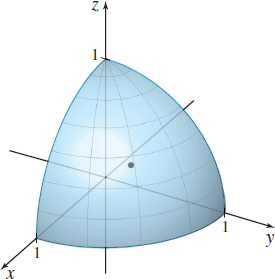
Find the centroid of the part of the unit sphere that lies in the first octant. See Figure 54.

Solution In spherical coordinates, the equation of the unit sphere \(S\): \(x^{2}+y^{2}+z^{2}=1\) is \(\rho =1.\) So using \(x=\cos \theta \sin \phi \), \(y=\sin \theta \sin \phi \), and \(z=\cos \phi\), we obtain the parametrization \[ \mathbf{r}=\mathbf{r}\left( \theta ,\phi \right) =\cos \theta \sin \phi \, \mathbf{i}+\sin \theta \sin \phi \,\mathbf{j}+\cos \phi\, \mathbf{k};\qquad 0\leq \theta \leq \dfrac{\pi }{2},\quad 0\leq \phi \leq \dfrac{\pi }{2} \]

We seek \(\left\Vert \mathbf{r}_{\theta }\times \mathbf{r}_{\phi }\right\Vert \) and \(dS.\) The partial derivatives of \(\mathbf{r}=\mathbf{r}\left( \theta ,\phi \right) \) are \[ \begin{eqnarray*} \mathbf{r}_{\theta }&=&-\sin \theta \sin \phi \,\mathbf{i}+\cos \theta \sin \phi \,\mathbf{j} \,\quad \mathbf{r}_{\phi }=\cos \theta \cos \phi \,\mathbf{i}+\sin \theta \cos \phi \,\mathbf{j}-\sin \phi\, \mathbf{k}\\[4pt] \mathbf{r}_{\theta }\times \mathbf{r}_{\phi } &=&\left|\begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] -\sin \theta \sin \phi & \cos \theta \sin \phi & 0 \\[3pt] \cos \theta \cos \phi & \sin \theta \cos \phi & -\sin \phi \end{array}\right|\\[4pt] &=&-\cos \theta \sin ^{2}\phi \,\mathbf{i}-\sin \theta \sin ^{2}\phi \,\mathbf{ j}-\sin \phi \cos \phi\, \mathbf{k} \\[4pt] \left\Vert \mathbf{r}_{\theta }\times \mathbf{r}_{\phi }\right\Vert &=&\sqrt{ \cos ^{2}\theta \sin ^{4}\phi +\sin ^{2}\theta \sin ^{4}\phi +\sin ^{2}\phi \cos ^{2}\phi }\\[4pt] &=&\sqrt{( \cos ^{2}\theta +\sin ^{2}\theta ) \sin ^{4}\phi +\sin ^{2}\phi \cos ^{2}\phi } \\[4pt] &=&\sqrt{\sin ^{2}\phi (\sin ^{2}\phi +\cos ^{2}\phi) }=\sin \phi\\[4pt] dS&=&\left\Vert \mathbf{r}_{\theta }\times \mathbf{r}_{\phi }\right\Vert d\theta\, d\phi =\sin \phi \,d\theta \,d\phi \end{eqnarray*} \]

1030

Since the surface area \(S\) of a sphere is \(S=4\pi r^{2},\) the surface area of the part of the unit sphere \(r=1\) in the first octant is \(\dfrac{1}{8}S=\dfrac{\pi }{2},\) so the mass \(M\) is \(\dfrac{\pi }{2}.\) Because of symmetry, \(\overline{x}=\overline{y}=\overline{z},\) so we need to find only one moment, say \(M_{xy}.\) \[ \begin{eqnarray*} M_{xy}&=&\iint\limits_{\kern-3ptS}z\,dS=\iint\limits_{\kern-3ptS}\cos \phi \,dS=\int_{0}^{\pi /2}\int_{0}^{\pi /2}\cos \phi\, \sin \phi\, d\theta\, d\phi\\[4pt] &=&\int_{0}^{\pi /2}\dfrac{\pi }{2}\cos \phi\, \sin \phi\, d\phi =\dfrac{\pi }{2}\left[ \dfrac{\sin ^{2}\phi }{2}\right] _{0}^{\pi /2}=\dfrac{\pi }{4} \end{eqnarray*} \]

The centroid of the part of the unit sphere in the first octant is \[ \left( \overline{x},\overline{y},\overline{z}\right) =\left( \dfrac{M_{yz}}{M },\dfrac{M_{xz}}{M},\dfrac{M_{xy}}{M}\right) =\left( \dfrac{1}{2},\dfrac{1}{2},\dfrac{1}{2} \right) \]