Finding the Orientations of a Surface

Find both orientations for the paraboloid defined by \(z=9-x^{2}-y^{2},\) \(z\geq 0.\)

1. Use rectangular coordinates to find the unit normal vectors.
2. Parametrize the surface, and then find the unit normal vectors.

Solution (a) Since the paraboloid is given by \(f(x,y) = 9-x^{2} - y^{2}, z \ge 0\), we can use the equations (3) and (4) to find the unit normal vectors. We begin by finding the partial derivatives \[ f_{x}(x,y) =-2x \qquad f_{y}(x,y) =-2y \]

Then \[ \begin{eqnarray*} \mathbf{n}&=&\dfrac{2x\,\mathbf{i}+2y\,\mathbf{j}+\mathbf{k}}{\sqrt{[-2x]^{2}+[-2y]^{2}+1}}=\dfrac{2x\,\mathbf{i}+2y\,\mathbf{j}+\mathbf{k}}{\sqrt{4x^{2}+4y^{2}+1}} \\[7pt] -\mathbf{n}&=&\dfrac{-2x\,\mathbf{i-}2y\,\mathbf{j}-\mathbf{k}}{\sqrt{[-2x]^{2}+[-2y]^{2}+1}}=\dfrac{ -2x\,\mathbf{i}-2y\,\mathbf{j}-\mathbf{k}}{\sqrt{4x^{2}+4y^{2}+1}} \end{eqnarray*} \]

Notice that the \(\mathbf{k}\) component of \(\mathbf{n}\) is positive, indicating \(\mathbf{n}\) is the upward-pointing unit normal vector.

(b) We parametrize \(z=9-x^{2}-y^{2},\) \(z\geq 0\), using cylindrical coordinates, by defining the parametric equations \[ \begin{equation*} x=r\cos \theta \qquad y=r\sin \theta \qquad z=9-(x^{2}+y^{2}) =9-r^{2} \end{equation*} \]

Then the parametrization is \[ \begin{equation*} \mathbf{r}=\mathbf{r}( r,\theta ) =r\cos \theta \,\mathbf{i} +r\sin \theta \,\mathbf{j}+( 9-r^{2}) \mathbf{k} \end{equation*} \]

We seek \(\left\Vert \mathbf{r}_{r}\times \mathbf{r}_{\theta }\right\Vert \). The partial derivatives of \(\mathbf{r}\) are \[ \begin{eqnarray*} \mathbf{r}_{r}&=&\cos \theta \,\mathbf{i}+\sin \theta \,\mathbf{j}-2r\mathbf{k} \qquad \mathbf{r}_{\theta }=-r\sin \theta \,\mathbf{i}+r\cos \theta \,\mathbf{j}\\[4pt] \mathbf{r}_{r}\times \mathbf{r}_{\theta } &=& \left|\begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] \cos \theta & \sin \theta & -2r \\[3pt] -r\sin \theta & r\cos \theta & 0 \end{array}\right| =2r^{2}\cos \theta\, \mathbf{i}+2r^{2}\sin \theta\, \mathbf{j}+r\mathbf{k} \\[4pt] \left\Vert \mathbf{r}_{r}\times \mathbf{r}_{\theta }\right\Vert &=&\sqrt{ 4r^{4}\cos ^{2}\theta +4r^{4}\sin ^{2}\theta +r^{2}}=\sqrt{4r^{4}+r^{2}}=r \sqrt{4r^{2}+1} \end{eqnarray*} \]

The unit normal vectors are \[ \begin{eqnarray*} \mathbf{n}&=&\dfrac{\mathbf{r}_{r}\times \mathbf{r}_{\theta }}{\left\Vert \mathbf{r}_{r}\times \mathbf{r}_{\theta }\right\Vert }=\dfrac{2r^{2}\cos \theta\, \mathbf{i}+2r^{2}\sin \theta\, \mathbf{j}+r\mathbf{k}}{r\sqrt{4r^{2}+1}} =\dfrac{2r\cos \theta\, \mathbf{i}+2r\sin \theta\, \mathbf{j}+\mathbf{k}}{\sqrt{ 4r^{2}+1}}\\[4pt] -\mathbf{n}&=&\dfrac{-2r\cos \theta\, \mathbf{i} -2r\sin \theta\, \mathbf{j}-\mathbf{k}}{\sqrt{4r^{2}+1}} \end{eqnarray*} \]

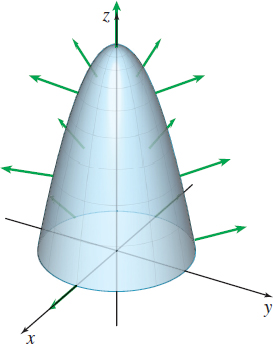
Notice that the unit vectors found in (a) and (b) are equivalent.