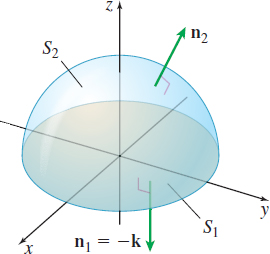
EXAMPLE 6Finding the Outer Unit Normal Vectors to a Surface S
Find the outer unit normal vectors to the solid E enclosed by z=f(x,y)=√R2−x2−y2andz=00≤x2+y2≤R2
Solution The solid E is the interior of a hemisphere with center at (0,0,0) and radius R as shown in Figure 62. The surface S consists of two surfaces, S1 and S2. The bottom surface S1 and top surface S2 are defined by S1:z=0andS2:z=f(x,y)=√R2−x2−y20≤x2+y2≤R2
The outer unit normal vector n1 of S1 is −k.
To find the outer unit normal vector n2 of S2, we find fx(x,y) and fy(x,y). fx(x,y)=−x√R2−x2−y2=−xzandfy(x,y)=−y√R2−x2−y2=−yz
Then n2=−fx(x,y)i−fy(x,y)j+k√[fx(x,y)]2+[fy(x,y)]2+1=xzi+yzj+k√x2z2+y2z2+1=xi+yj+zk√x2+y2+z2=xi+yi+zkR