Finding the Flux of \(\mathbf{F}\) Across a Cylinder

A fluid has a constant mass density \(\rho .\) Find the mass of fluid flowing across the cylinder \(x^{2}+y^{2}=4,\) where \(0\leq z\leq 3,\) in a unit of time in the direction outward from the \(z\)-axis, if the velocity of the fluid at any point on the cylinder is \(\mathbf{F}=\mathbf{F}(x,y,z)=x\mathbf{i} +y\mathbf{j}+2z\mathbf{k}\). That is, find the flux of \(\mathbf{F}\) across the cylinder.

Solution In cylindrical coordinates \(x^{2}+y^{2}=r^{2}=4,\) or equivalently, \(r=2,\) which leads to the parametrization \(\mathbf{r}\left( \theta ,z\right) =2\cos \theta \,\mathbf{i}+2\sin \theta \,\mathbf{j}+z\,\mathbf{k}\), \(0\leq \theta \leq 2\pi ,\) \(0\leq z\leq 3.\)

We seek \(\left\Vert \mathbf{r}_{\theta}\times \mathbf{r}_{z }\right\Vert \) and \(dS\).

The partial derivatives of \(\mathbf{r}\) are \[ \begin{eqnarray*} \mathbf{r}_{\theta }&=&-2\sin \theta \,\mathbf{i}+2\cos \theta \,\mathbf{j}\quad \quad \ \mathbf{r}_{z}=\mathbf{k}\\[4pt] \mathbf{r}_{\theta }\times \mathbf{r}_{z} &=& \left|\begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] -2\sin \theta & 2\cos \theta & 0 \\[3pt] 0 & 0 & 1 \end{array}\right| =2\cos \theta\, \mathbf{i}+2\sin \theta\, \mathbf{j} \\[4pt] \left\Vert \mathbf{r}_{\theta }\times \mathbf{r}_{z}\right\Vert &=&\sqrt{ 4\cos ^{2}\theta +4\sin ^{2}\theta }=2 \\[4pt] dS &=&\left\Vert \mathbf{r}_{\theta }\times \mathbf{r}_{z}\right\Vert d\theta \,dz=2\,d\theta \,dz \end{eqnarray*} \]

Then the unit normal vector \(\mathbf{n}\) is \[ \begin{equation*} \mathbf{n}=\dfrac{\mathbf{r}_{\theta}\times \mathbf{r}_{z}}{\left\Vert \mathbf{r}_{\theta}\times \mathbf{r}_{z}\right\Vert }=\dfrac{2\cos \theta\, \mathbf{i}+2\sin \theta\, \mathbf{j}}{2}=\cos \theta\, \mathbf{i}+\sin \theta\, \mathbf{j} \end{equation*} \]

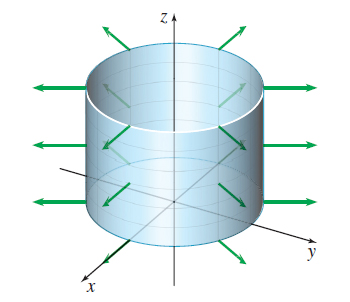
These vectors point outward from the surface of the cylinder, so we have the correct orientation. Figure 65 shows the cylinder \(x^{2}+y^{2}=4,\) where \(0\leq z\leq 3,\) and the outer unit normal vectors to the cylinder.

We now write \(\mathbf{F}\) using the parametrization. \[ \mathbf{F}=\mathbf{F}(x,y,z)=\mathbf{F}(\theta ,z)=2\cos \theta \,\mathbf{i} +2\sin \theta \,\mathbf{j}+2z\,\mathbf{k} \]

The velocity of the fluid in the direction of \(\mathbf{n}\) is \[ \begin{equation*} \mathbf{F\,{\cdot}\, n}=\left( 2\cos \theta \,\mathbf{i}+2\sin \theta \,\mathbf{j} +2z\,\mathbf{k}\right) \,{\cdot}\, \left( \cos \theta\, \mathbf{i}+\sin \theta\, \mathbf{j}\right) =2\cos ^{2}\theta \,+2\sin ^{2}\theta =2 \end{equation*} \]

The mass of fluid flowing across the cylinder \(x^{2}+y^{2}=4\) in a unit of time in the direction of \(\mathbf{n}\) is given by \[ \iint\limits_{\kern-3ptS}\rho \,\mathbf{F}\,{\cdot}\, \mathbf{n}\,dS=\int_{0}^{3} \int_{0}^{2\pi }\left( \rho \,2\right) 2\,d\theta \,dz=4\rho \int_{0}^{3}2\pi \,dz=\left( 8\rho \pi \right) 3=24\rho \pi \]

The flux of \(\mathbf{F}\) across \(S\) is \(24\rho \pi.\)