Using the Divergence Theorem to Find a Surface Integral

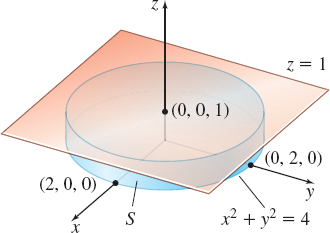
Let \(S\) be the surface of a cylindrical solid \(E\) whose boundary is \(x^{2}+y^{2}=4\), \(z=0\), and \(z=1\). Let \(\mathbf{F}=x^{3}\mathbf{i}+y^{3} \mathbf{j}+z^{2}\mathbf{k}\) and let \(\mathbf{n}\) be the outer unit normal to \(S\). Use the Divergence Theorem to find \(\iint\limits_S \mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS\).

Solution Figure 68 illustrates the cylindrical surface \(S\). We begin by finding \({\rm{div}}\mathbf{F}=3x^{2}+3y^{2}+2z\). Then we use the Divergence Theorem, obtaining \[ \iint\limits_{S}\mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS=\iiint \limits_{E}(3x^{2}+3y^{2}+2z)\,dV \]

Because \(E\) is a cylindrical solid, we use cylindrical coordinates: \[ 3x^{2}+3y^{2}+2z=3r^{2}\cos ^{2}\theta +3r^{2}\sin ^{2}\theta+ 2z=3r^{2}( \cos ^{2}\theta +\sin ^{2}\theta ) +2z=3r^{2}+2z \]

The solid \(E\) is given by \(0\leq r\leq 2\), \(0\leq \theta \leq 2\pi\) , \(0\leq z\leq 1\). Then \[ \begin{eqnarray*} \iint\limits_{S}\mathbf{F}\,{\cdot}\, \mathbf{n}\,ds& =&\iiint\limits_E(3x^{2}+3y^{2}+2z)\,dV \underset{\underset{\color{#0066A7}{dV=r\,dr\,d\theta \,dz}}{\color{#0066A7}{\uparrow}}} {=} \iiint\limits_E(3r^{2}+2z)\,r\,dr\,d\theta dz \\ &=&\int_{0}^{2\pi }\int_{0}^{2}\int_{0}^{1}(3r^{3}+2rz)\,dz\,dr\,d\theta \\ & =&\int_{0}^{2\pi }\int_{0}^{2}\big[ 3r^{3}z+r z^{2}\big] _{0}^{1}\,dr\,d\theta =\int_{0}^{2\pi }\int_{0}^{2}(3r^{3}+r)\,dr\,d\theta\\ &=&\int_{0}^{2\pi }\left[ \dfrac{3r^{4}}{4}+\dfrac{r^{2}}{2}\right] _{0}^{2}\,d\theta =\int_{0}^{2\pi }14\,d\theta =28\pi \end{eqnarray*} \]