Using the Divergence Theorem to Find a Surface Integral

Let \(\mathbf{F}(x,y,z)=x^{3}\mathbf{i}+y^{3}\mathbf{j}+z^{3}\mathbf{k}\). If \(S\) is the surface of the spherical solid \(E\) in the first octant enclosed by \(z=\sqrt{ 4-x^{2}-y^{2}}\) and \(z=0\), and \(\mathbf{n}\) is the outer unit normal to \(S\), use the Divergence Theorem to find \(\iint\limits_S \mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS\).

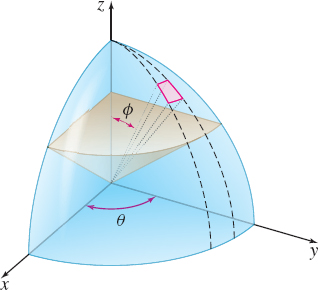
Solution See Figure 69. Since \({\rm{div}}\mathbf{F} =3x^{2}+3y^{2}+3z^{2}=3(x^{2}+y^{2}+z^{2})\), we use the Divergence Theorem, obtaining \[ \iint\limits_{S}\mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS=3\iiint \limits_E(x^{2}+y^{2}+z^{2})\,dV \]

We use spherical coordinates to find the triple integral. Then \(x^{2}+y^{2}+z^{2}=\rho ^{2}\) and \(dV=\rho ^{2}\sin \phi \,d\rho \,d\theta \,d\phi\). The solid \(E\) is given by \(0\leq \rho \leq 2\), \(0\leq \theta \leq \dfrac{\pi}{2}\), \(0\leq \phi \leq \dfrac{\pi }{2}\). Then \[ \begin{eqnarray*} \iint\limits_{S}\mathbf{F}\,{\cdot}\, \mathbf{n}\,dS &= &3\iiint\limits_E \rho ^{2}( \rho ^{2}\sin \phi \,d\rho \,d\theta \,d\phi ) = 3\int_{0}^{\pi /2}\int_{0}^{\pi /2 }\int_{0}^{2}\rho ^{4}\,\sin \phi \,d\rho \,d\theta \,d\phi \notag \\ &=&3\int_{0}^{\pi /2}\int_{0}^{\pi /2}\left[ \dfrac{\rho ^{5}}{5}\right] _{0}^{2}\sin \phi\, d\theta \,d\phi =3\int_{0}^{\pi /2}\int_{0}^{\pi /2 }\dfrac{ 32}{5}\sin \phi\, d\theta \,d\phi \\ &=&\dfrac{96}{5}\int_{0}^{\pi /2}\big[ \theta \big] _{0}^{\pi /2}\sin \phi \,d\phi \notag \\ &=&\dfrac{48\pi }{5}\int_{0}^{\pi /2}\sin \phi \,d\phi =\dfrac{48\pi }{5} \big[ -\cos \phi \big] _{0}^{\pi /2}=\dfrac{48\pi }{5} \end{eqnarray*} \]