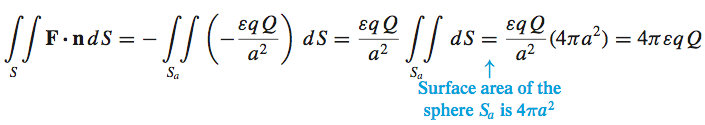Applying the Divergence Theorem to an Electric Force Field
Let \(\mathbf{F}=\mathbf{F}(x,y,z)\) be an electric force field \[ \mathbf{F}=\mathbf{F}(x,y,z)=\frac{\varepsilon qQ}{x^{2}+y^{2}+z^{2}}\mathbf{u} \]
where \(\varepsilon \) is a constant that depends on the units used; \(q\) and \(Q \) are the charges of two objects, one located at the point \((0,0,0)\) and the other at a point \((x,y,z)\); and \(\mathbf{u}\) is the unit vector in the direction from \((0,0,0)\) to \((x,y,z)\). Let \(S\) be a closed surface with positive orientation that encloses a solid \(E \) in space.
Show that the following statements are true under the assumptions of the Divergence Theorem:
- If neither \(S\) nor its interior contains the point \((0,0,0)\), then \(\iint\limits_S \mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS=0\). That is, the flux of \(\mathbf{F}\) across \(S\) equals \(0\).
- If the interior of \(S\) contains the point \((0,0,0)\), then \(\iint\limits_S \mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS=4\pi \varepsilon qQ\). That is, the flux of \(\mathbf{F}\) across \(S\) equals \(4\pi \varepsilon qQ\).
The electric force field \(\mathbf{F}\) is continuous everywhere except at the point \((0,0,0)\).
(a) The surface \(S\) that forms the boundary of the solid \(E \) satisfies the assumptions of the Divergence Theorem. We find \({\rm{div}} \mathbf{F}\). \[ \begin{eqnarray*} {\rm{div}}\mathbf{F}&= &\varepsilon qQ\left\{\dfrac{\partial }{\partial x}\left[ \dfrac{x}{ (x^{2}+y^{2}+z^{2})^{3/2}}\right] +\dfrac{\partial }{\partial y}\left[ \dfrac{y }{(x^{2}+y^{2}+z^{2})^{3/2}}\right] +\dfrac{\partial }{\partial z}\left[ \dfrac{z}{(x^{2}+y^{2}+z^{2})^{3/2}}\right] \right\} \\ &=&\varepsilon qQ\bigg\{\dfrac{(x^{2}+y^{2}+z^{2})^{3/2}-3x^{2} \sqrt{x^{2}+y^{2}+z^{2}}}{(x^{2}+y^{2}+z^{2})^{3}}+\dfrac{ (x^{2}+y^{2}+z^{2})^{3/2}-3y^{2}\sqrt{x^{2}+y^{2}+z^{2}}}{ (x^{2}+y^{2}+z^{2})^{3}} \\ &&+\,\dfrac{(x^{2}+y^{2}+z^{2})^{3/2}-3z^{2}\sqrt{x^{2}+y^{2}+z^{2}}}{ (x^{2}+y^{2}+z^{2})^{3}} \bigg\} \\ &=&\varepsilon qQ\dfrac{3(x^{2}+y^{2}+z^{2})^{3/2}-3\sqrt{x^{2}+y^{2}+z^{2}}(x^{2}+y^{2}+z^{2})}{(x^{2}+y^{2}+z^{2})^{3}}=0 \end{eqnarray*} \]
Therefore, by the Divergence Theorem, \[ \iint\limits_{S}\mathbf{F}\,{\cdot}\, \mathbf{n}\,dS=\iiint\limits_E {\rm{div}} \mathbf{F}\,dV=0 \]
(b) Since the interior of \(S\) contains the origin, \(\mathbf{F}\) is not continuous at the origin, so we cannot use the Divergence Theorem. We use the following argument to prove (b). Let \(E \) be the closed solid enclosed by two separate surfaces: the surface \(S\) and a sphere \(S_{a}\) of radius \(a\), with its center at \((0,0,0)\), as shown in Figure 70. The outer surface is \(S\) and the inner surface is \(S_{a}\). Now \(\mathbf{F}\) is continuous throughout \(E\), so the Divergence Theorem can be used. \[ \iiint\limits_E {\rm{div}}\mathbf{F}\,dV=\iint\limits_{S}\mathbf{F}\,{\cdot}\, \mathbf{n}\,dS+\iint\limits_{S_{a}}\mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS \]
1044
From (a), we know that \(\iiint\limits_{E}{\rm{div}}\mathbf{F}\,dV=0\). So, \[ \iint\limits_{S}\mathbf{F}\,{\bf\cdot}\, \mathbf{n}\,dS=-\iint\limits_{S_{a}}\mathbf{F }\,{\bf\cdot}\, \mathbf{n}\,dS \]
On the inner surface \(S_{a}\), a sphere of radius \(a\), the outer unit normal is \[ \mathbf{n}=-\dfrac{x\mathbf{i}+y\mathbf{j}+z\mathbf{k}}{a}=-\dfrac{x\mathbf{i}+ y\mathbf{j}+z\mathbf{k}}{\sqrt{x^{2}+y^{2}+z^{2}}} \]
Then \[ \begin{eqnarray*} \mathbf{F}\,{\bf\cdot}\, \mathbf{n\,} &=&\dfrac{\varepsilon qQ}{x^{2}+y^{2}+z^{2}} \mathbf{u}\,{\bf\cdot}\, \left( -\dfrac{x\mathbf{i}+y\mathbf{j}+z\mathbf{k}}{\sqrt{ x^{2}+y^{2}+z^{2}}}\right)\\ &=&-\dfrac{\varepsilon qQ}{x^{2}+y^{2}+z^{2}}\dfrac{x \mathbf{i}+y\mathbf{j}+z\mathbf{k}}{\sqrt{x^{2}+y^{2}+z^{2}}}\,{\bf\cdot}\, \dfrac{x \mathbf{i}+y\mathbf{j}+z\mathbf{k}}{\sqrt{x^{2}+y^{2}+z^{2}}} \\ &=&-\varepsilon qQ\dfrac{x^{2}+y^{2}+z^{2}}{a^{4}}=-\dfrac{\varepsilon qQ}{ a^{2}} \end{eqnarray*} \]
So,