Verifying Stokes' Theorem

Verify Stokes' Theorem for \(\mathbf{F}=y\mathbf{i}-x\mathbf{j}\), where the surface \(S\) is the paraboloid \(z=x^{2}+y^{2}\), with \(x^{2}+y^{2}=1\), \(z=1 \), as its boundary \(C\).

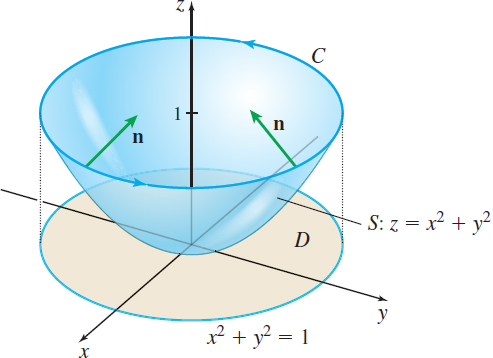
Solution  Figure 72 shows the paraboloid and the circle \(C\) in the plane \(z=1\). Stokes' Theorem states the following: \[ \oint\limits_{C}\mathbf{F}\,{\bf\cdot}\, d\mathbf{r}=\iint\limits_{\kern-3ptS}{\rm{curl}\, \mathbf{F} \,{\bf\cdot}\, \mathbf{n}}\,dS \]

Parametric equations for \(C\) are \(x=\cos t\), \(y=\sin t\), \(z=1,\) \( 0\leq t\leq 2\pi\). We use the parametric equations to find the line integral \(\oint_{C}\mathbf{F}\,{\bf\cdot}\, d\mathbf{r}\) for \(\mathbf{F}=y\mathbf{i}-x \mathbf{j}\). \[ \begin{eqnarray*} \oint_{C}\mathbf{F}\,{\bf\cdot}\, d\mathbf{r}&=&\oint_{C}(y\,dx-x\,dy)=\int_{0}^{2\pi } \left[ \sin t\left( -\sin t\,dt\right) -\cos t\cos t\,dt\right]\\[4pt] &=&-\int_{0}^{2\pi }[\sin ^{2}t+\cos ^{2}t]\,dt=-\int_{0}^{2\pi }dt=-2\pi \end{eqnarray*} \]

To find the surface integral, \(\iint\limits_{\kern-3ptS}{\rm{curl}\, \mathbf{F}\,{\bf\cdot}\, \mathbf{n}}\,dS\), we find \(\rm{curl}\, \mathbf{F}\) and \(\mathbf{n}\): \[ \begin{eqnarray*} \rm{curl}\, \mathbf{F} &\mathbf{=}&\left\vert \begin{array}{@{}c@{\quad}c@{\quad}c} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] \dfrac{\partial }{\partial x} & \dfrac{\partial }{\partial y} & \dfrac{\partial }{\partial z} \\[5pt] P & Q & R \end{array} \right\vert =\left\vert \begin{array}{@{}c@{\quad}c@{\quad}c} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] \dfrac{\partial }{\partial x} & \dfrac{\partial }{\partial y} & \dfrac{\partial }{\partial z} \\[5pt] y & -x & 0 \end{array} \right\vert \\[4pt] &=&\left[ \dfrac{\partial }{\partial y}0-\dfrac{\partial }{\partial z}(-x) \right] \,\mathbf{i}-\left[ \dfrac{\partial }{\partial x}0-\dfrac{\partial }{ \partial z}y\right] \,\mathbf{j}+\left[ \dfrac{\partial }{\partial x}(-x)- \dfrac{\partial }{\partial y}y\right] \mathbf{k}\\[4pt] &=&0\mathbf{i}-0\mathbf{j}-2\mathbf{k}=-2\mathbf{k} \end{eqnarray*} \]

1048

For \(z=f(x,y) =x^{2}+y^{2}\), we have \[ \begin{eqnarray*} \mathbf{n\,} &=& \tfrac{-f_{x}(x,y)\mathbf{i}-f_{y}(x,y) \mathbf{j\,}+\,\mathbf{k}}{\sqrt{[f_{x}(x,y)]^{2}+[f_{y}(x,y)]^{2}+1}} = \dfrac{-2x\mathbf{i}-2y\mathbf{j}+\mathbf{k}}{\sqrt{ 4x^{2}+4y^{2}+1}}\\[4pt] \rm{curl}\, \mathbf{F}\,{\bf\cdot}\, \mathbf{n} &=&-2\mathbf{k\,{\bf\cdot}\, }\dfrac{1}{\sqrt{ 4x^{2}+4y^{2}+1}}\left( -2x\mathbf{i}-2y\mathbf{j}+\mathbf{k}\right) =\dfrac{ -2}{\sqrt{4x^{2}+4y^{2}+1}} \end{eqnarray*} \] So,

where \(D\) is the interior of the circle \(x^{2}+y^{2}=1\).