Figure

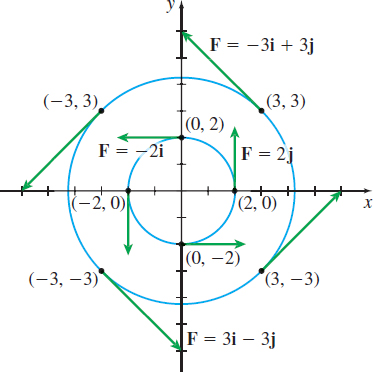
EXAMPLE 1Describing a Vector Field in the Plane

Describe the vector field $\mathbf{F}=\mathbf{F}(x,y)=-y\mathbf{i}+x\mathbf{j}$ by drawing some of the vectors $\bf{F}.$

We begin by making a table of vectors. We do this by choosing points $(x,y)$ and finding the values of $\bf{F.}$

$(x,y)$	$( 2,0)$	$( 0,2)$	$( -2,0)$	$( 0,-2)$	$( 3,3)$	$( -3,3)$	$( -3,-3)$	$( 3,-3)$
$\mathbf{F}(x,y)$	$\ 2\mathbf{j}$	$-2\mathbf{i}$	$-2\mathbf{j}$	$2\mathbf{i}$	$-3\mathbf{i}+3\mathbf{j}$	$-3\mathbf{i}-3\mathbf{j}$	$3\mathbf{i}-3\mathbf{j}$	$3\mathbf{i}+3\mathbf{j}$

Figure 3

Figure 3 illustrates the vectors from the table. Notice that each vector in the field is tangent to a circle centered at the origin, and the direction of the vectors indicates that the field is rotating counterclockwise. This field might represent the motion of a wheel spinning on an axle, with each vector equal to the velocity at a point of the wheel.