EXAMPLE 6Describing a Gradient Vector Field
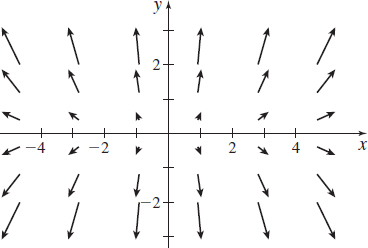
Figure 8 \boldsymbol\nabla\! f = 2x\mathbf{i}+8y\mathbf{j}
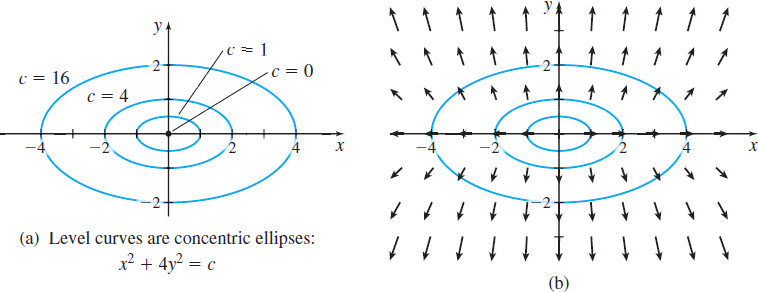
- (a) Find the gradient vector field of f(x,y)=x^{2}+4y^{2} and graph it by drawing some of the vectors \boldsymbol\nabla\! f.
- (b) Graph the level curves f(x,y)=c, for c=0,1,4, and 16.
Solution (a) The gradient of f is \boldsymbol\nabla\! f=\dfrac{\partial f}{\partial x}\,\mathbf{i}+\dfrac{\partial f}{\partial y}\,\mathbf{j}=2x\mathbf{i}+8y\mathbf{j}. The graph of the gradient vector field is shown in Figure 8.
(b) Figure 9(a) illustrates the level curves of the elliptic paraboloid f(x, y)=x^{2}+4y^{2}=c for c=0,1,4, and 16. Compare the level curves with the gradient vector field illustrated in Figure 8. Notice that the gradient vectors are orthogonal to the level curves, as shown in Figure 9(b).