Find $\int_{C}y\,ds$ if $C$ is the curve defined by the parametric equations $x(t)=t$ and $y(t)=\sqrt{t}$, $2\leq t\leq 6$

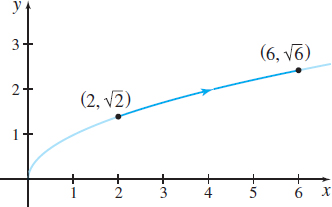
Figure 13 $x(t)=t, y(t)=\sqrt{t}$, $2\leq t\leq 6$

Solution The curve $C$ is smooth and is part of the graph of $y=\sqrt{x}$, from $(2,\sqrt{2})$ to $(6,\sqrt{6})$, as shown in Figure 13.

The differential $ds$ of arc length along $C$ is given by $$ds=\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}\,dt$$

Since $\dfrac{dx}{dt}=1$ and $\dfrac{dy}{dt}=\dfrac{1}{2\sqrt{t}},$ we have $$ds=\sqrt{1^{2}+\left( \dfrac{1}{2\sqrt{t}}\right) ^{2}}\,dt=\sqrt{1+\dfrac{1}{4t}}\,dt=\sqrt{\dfrac{4t+1}{4t}}\,dt=\dfrac{\sqrt{4t+1}}{2\sqrt{t}}\,dt$$

Now we use formula (1). $$\int_{C}y\,ds\underset{\underset{\color{#0066A7}{\hbox{\(y=\sqrt{t}\)}}}{\color{#0066A7}{\uparrow}}}{=}\int_{2}^{6}\sqrt{t}\dfrac{\sqrt{4t+1}}{2\sqrt{t}}\,dt=\dfrac{1}{2}\int_{2}^{6}\sqrt{4t+1}\,dt=\dfrac{1}{2}\left[ \dfrac{(4t+1)^{3/2}}{4\,{\cdot}\, \dfrac{3}{2}}\right] _{2}^{6}=\dfrac{49}{6}$$