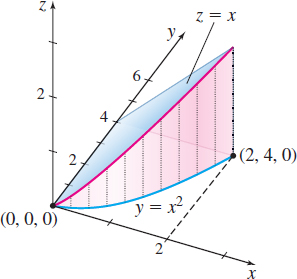
Finding the Lateral Surface Area of a Cylinder

Find the lateral surface area \(A\) of the cylinder that lies above the \(xy\)-plane, below the surface \(z = f(x,y)=x,\) and formed by lines parallel to the \(z\) -axis that intersect the curve \(y=x^{2}\), \(0\leq x\leq 2\).

Solution Figure 17 illustrates the cylinder. Along \(C\), \(y=x^{2},\) the differential \(ds\) of arc length is \[ ds=\sqrt{1+\left( \dfrac{dy}{dx}\right) ^{2}}\,dx\underset{ \underset{\color{#0066A7} {\hbox{\(\dfrac{dy}{dx}=2x\)}}} {\color{#0066A7}{\uparrow }}}{=} \sqrt{1+4x^{2}}\,dx\\[-11pt] \]

The lateral surface area \(A\) of the cylinder is \[ \begin{eqnarray*} A& =&\int_{C}f(x,y) ds=\int_{C}x\,ds=\int_{0}^{2}x\sqrt{1+4x^{2}} \,dx \qquad \color{#0066A7}{{\rm Let}\ u=1+4x^{2};\ {\rm then}\ du=8x\,dx\ {\rm or} \ x\,dx= \dfrac{1}{8}\, du.}\\ && \hspace{14.5pc}\color{#0066A7}{\hbox{When \(x=0\), \(u=1\); when \(x=2\), \(u=17\).}} \\ & =&\int_{1}^{17}\dfrac{1}{8}\sqrt{u}\,du=\left[ \dfrac{1}{4}\dfrac{u^{3/2}}{3}\right] _{1}^{17}=\dfrac{17\sqrt{17}-1}{12} \end{eqnarray*} \]