Finding a Line Integral of the Form \(\int_{C}( P\,dx+Q\,dy)\)

Find the line integral \(\int_{C}(y^{2}\,dx-x^{2}\,dy)\) along

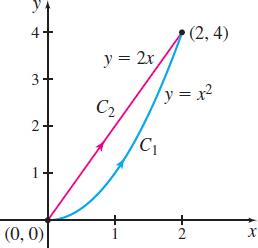
\(C_{1}\): The parabola \(y=x^{2}\) joining the two points \((0,0)\) and \((2,4)\)

\(C_{2}\): The line \(y=2x\) joining the two points \((0,0)\) and \((2,4)\)

Solution The curves \(C_{1}\) and \(C_{2}\) are smooth, and the functions \(P(x,y) =y^{2}\) and \(Q(x,y) = -x^{2}\) are continuous in the \(xy\)-plane.

Along \(C_{1},\) parametric equations for the parabola are \(x(t) =t,\) \(y(t) =t^{2}.\) Then \(dx=dt\) and \(dy=2t\,dt,\) so \[ \begin{eqnarray*} \int_{C_{1}}(y^{2}\,dx-x^{2}\,dy)&=&\int_{C_{1}}y^{2}\,dx-\int_{C_{1}}x^{2}\,dy=\int_{0}^{2}(t^2) ^{2}\,dt-\int_{0}^{2}t^{2}(2t\,dt)\\ &=& \int_{0}^{2}t^{4}\,dt-2\int_{0}^{2}t^{3}\,dt=\left[ \dfrac{t^{5}}{5}\right] _{0}^{2}-\left[ \dfrac{t^{4}}{2}\right] _{0}^{2}=-\dfrac{8}{5} \end{eqnarray*} \]

Along \(C_{2}\), parametric equations for the line segment are \(x(t) =t\), \(y(t) =2t.\) Then \(dx=dt\) and \(dy=2\,dt,\) so \[ \begin{eqnarray*} \int_{C_{2}}(y^{2}\,dx-x^{2}\,dy)&=&\int_{C_{2}}y^{2}\,dx-\int_{C_{2}}x^{2}\,dy=\int_{0}^{2}(2t) ^{2}\,dt-\int_{0}^{2}t^{2}(2\,dt)\\[4pt] &=& \left[ \dfrac{4t^{3}}{3}\right] _{0}^{2}-\left[ \dfrac{2t^{3}}{3}\right] _{0}^{2}=\dfrac{16}{3} \end{eqnarray*} \]

Figure 18 shows the curves \(C_{1}\) and \(C_{2}\) joining the points \(( 0,0) \) and \((2,4) .\)