Find the family of orthogonal trajectories for the one-parameter family $y^{2}=Cx^{3}$. See Figure 3 for several graphs in the family.

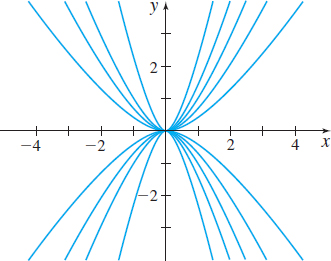
Figure 3 $y^{2}=Cx^{3}$

Solution

Step 1 We differentiate $y^{2}=Cx^{3}$ with respect to $x$. $$2yy^{\prime} =3Cx^{2}$$

Then we eliminate $C$ using this equation and the equation $y^{2}=Cx^{3}$ of the family. Since $C=\dfrac{y^{2}}{x^{3}},$ we find $$\begin{eqnarray*} 2yy^{\prime} & =&3\frac{y^{2}}{x^{3}}x^{2} \\ y^{\prime} & =&\frac{3y}{2x} \end{eqnarray*}$$

Step 2 Now we replace $y^{\prime}$ with $-\dfrac{1}{y^{\prime} },$ to obtain the differential equation for the family of orthogonal trajectories. $$\begin{eqnarray*} -\dfrac{1}{y^{\prime} }& =&\frac{3y}{2x} \\ y^{\prime} & =&-\frac{2x}{3y} \end{eqnarray*}$$

1068

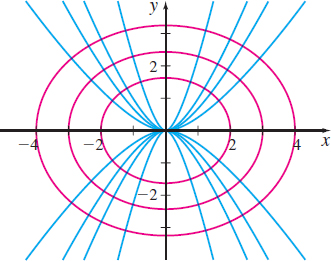
Figure 4
Blue: $y^{2}=Cx^{3};$
Pink: $x^{2}+\dfrac{3}{2}y^{2}=k$

Step 3 The differential equation $\dfrac{dy}{dx}=-\dfrac{2x}{3y}$ is separable and can be written as $$\begin{equation*} 2x\,dx+3y\,dy=0 \end{equation*}$$

The general solution is $$\begin{equation*} x^{2}+\frac{3}{2}y^{2}=K \end{equation*}$$

The orthogonal trajectories for the family $y^{2}=Cx^{3}$ is a family of ellipses $x^{2}+\dfrac{3}{2}y^{2}=K$, as shown in Figure 4.