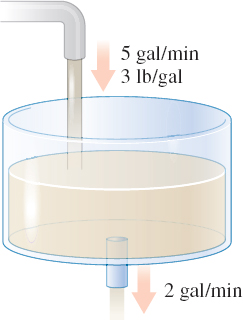
Solving a Flow Rate Problem

A large tank contains \(81\;\rm{gal}\) of brine in which \(20\;\rm{lb}\) of salt are dissolved. Brine containing \(3\;\rm{lb}\) of dissolved salt per gallon runs into the tank at the rate of \(5\;\rm{gal}/\rm{min}\). The mixture, kept uniform by stirring, drains from the tank at the rate of \(2 \;\rm{gal}/\rm{min}\). How much salt is in the tank at the end of \(37 \;\rm{min}\)? See Figure 6.

Solution Let \(y(t)\) be the amount of salt in the tank at time \(t\) . The rate of change \(\dfrac{dy}{dt}\) of salt in the tank at time \(t\) is the rate at which salt enters the tank minus the rate at which salt leaves the tank. Salt enters the tank at the rate of \(\left( 3\;\rm{lb}/\rm{gal}\right) \left(5\;\rm{gal}/\rm{min}\right) =15\;\rm{lb}/\rm{min}\).

To find the rate at which the salt exits the tank, we first need to find the concentration of salt in pounds per gallon at time \(t\). \[ \begin{equation*} \hbox{Concentration}=\dfrac{\hbox{amount of salt}}{\hbox{number of gallons}}= \frac{y(t)}{81+(5-2)t}=\dfrac{y( t) }{81+3t}\;\rm{lb}/\rm{gal} \end{equation*} \]

Then the rate at which the salt exits the tank is \[ \begin{equation*} \left( \dfrac{y( t) }{81+3t}\;\rm{lb}/\rm{gal}\right) \left( 2 \;\rm{gal}/\rm{min}\right) =\dfrac{2y( t) }{81+3t}\;\rm{lb}/\rm{min} \end{equation*} \]

The mixture problem is modeled by the differential equation \[ \begin{eqnarray*} \dfrac{dy}{dt}=\hbox{rate in }-\hbox{rate out}&=&15-\frac{2y( t) }{ 81+3t}\\ \dfrac{dy}{dt}+\frac{2}{3( 27+t) }y&=&15 \end{eqnarray*} \]

This is a first-order linear differential equation. We use the integrating factor: \[ \begin{eqnarray*} e^{\int \!P( t)\,dt}&=&\exp \!\left[ \int \!\dfrac{2}{3( 27+t) } dt\right] =\exp \!\left[ \dfrac{2}{3}\ln ( 27+t) \right]\\ &=&\exp\,[ \ln ( 27+t) ^{2/3}] =(27+t)^{2/3} \end{eqnarray*} \]

We multiply the differential equation by the integrating factor to obtain \[ \begin{eqnarray*} (27+t)^{2/3}\dfrac{dy}{dt}+\dfrac{2y}{3( 27+t) ^{1/3}} &=&15(27+t)^{2/3} \\ \frac{d}{dt}[y(t)(27+t)^{2/3}] &=&15(27+t)^{2/3} \end{eqnarray*} \]

Now we integrate both sides with respect to \(t\).

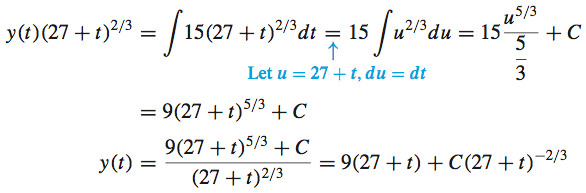
1082

Next we use the initial condition that \(y( 0) =20\;\rm{lb}\). Then \[ \begin{eqnarray*} y( 0) &=&20=9(27)+C(27)^{-2/3}\\ -223 &=&\dfrac{C}{9} \\ C &=&-2007 \end{eqnarray*} \]

The amount of salt \(y( t) \) in the brine at time \(t\) min is \[ \begin{equation*} y(t)=9(27+t)-2007(27+t)^{-2/3} \end{equation*} \]

The amount of salt in the tank at the end of \(37\;\rm{min}\) is \[ y(37)=9(27+37)-2007(27+37)^{-2/3}\approx 451\;\rm{lb} \]