EXAMPLE 1Finding the Values of an Inverse Sine Function
Find the exact value of:
- (a) sin−1√32
- (b) sin−1(−√22)
- (c) sin−1(sinπ8)
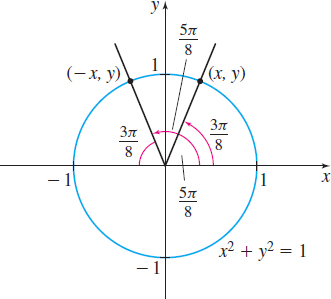
- (d) sin−1(sin5π8)
Solution (a) We seek an angle whose sine is √32. Since −1<√32<1, let y=sin−1√32. Then by definition, siny=√32, where −π2≤y≤π2. Although siny=√32 has infinitely many solutions, the only number in the interval [−π2,π2], for which siny=√32, is π3. So sin−1√32=π3.
(b) We seek an angle whose sine is −√22. Since −1<−√22<1, let y=sin−1(−√22). Then by definition, siny=−√22, where −π2≤y≤π2. The only number in the interval [−π2,π2], whose sine is −√22, is −π4. So sin−1(−√22)=−π4.
(c) Since the number π8 is in the interval [−π2,π2], we use (1). sin−1(sinπ8)=π8
(d) Since the number 5π8 is not in the closed interval [−π2,π2], we cannot use (1). Instead, we find a number x in the interval [−π2,π2] for which sinx=sin5π8. Using Figure 84, we see that sin5π8=y=sin3π8. The number 3π8 is in the interval [−π2,π2], so sin−1(sin5π8)=sin−1(sin3π8)=3π8