Write $\sin ( \tan ^{-1}u)$ as an algebraic expression containing $u.$

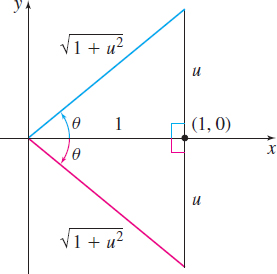
Figure 88 $\tan \theta =u$; $-\dfrac{\pi }{2}<\theta < \dfrac{\pi }{2}$.

Solution Let $\theta =\tan ^{-1}u$ so that $\tan \theta =u$, where $-\dfrac{\pi }{2}<\theta <\dfrac{\pi }{2}$. We note that in the interval $\left( -\dfrac{\pi }{2},\dfrac{\pi }{2}\right) ,$ $\sec \theta >0.$ Then $$\begin{array}{l} \sin (\tan ^{ - 1} u) = \sin \theta = \sin \theta \cdot \frac{{\cos \theta }}{{\cos \theta }} = \tan \theta \cos \theta \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\tan \theta }}{{\sec \theta }} = \frac{{\tan \theta }}{{\sqrt {1 + \tan ^2 \theta } }} = \frac{u}{{\sqrt {1 + u^2 } }} \\ {\color{#0066A7}{ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\sec ^2 \theta = 1 + \mathop {\tan ^2 }\limits^ \uparrow \theta ;\sec \theta > 0}} \\ \end{array}$$

An alternate method of obtaining the solution to Example 2 uses right triangles. Let $\theta =\tan ^{-1}u$ so that $\tan \theta =u$, $- \dfrac{\pi }{2}<\theta <\dfrac{\pi }{2}$, and label the right triangles drawn in Figure 88. Using the Pythagorean Theorem, the hypotenuse of each triangle is $\sqrt{1+u^{2}}.$ Then $\sin (\tan ^{-1}u) =\sin \theta =\dfrac{u}{\sqrt{1+u^{2}}}.$