Analyzing a Piecewise-Defined Function

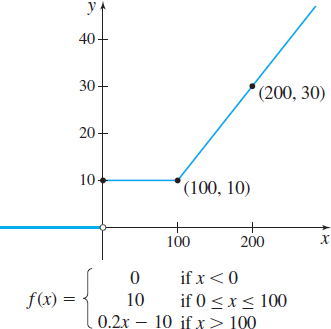
The function \(f\) is defined as \[ f( x) =\left\{ \begin{array}{c@{\qquad}l} 0 & \hbox{if }x \lt 0 \\ 10 & \hbox{if }0\leq x\leq 100 \\ 0.2x-10 & \hbox{if }x \gt 100 \end{array} \right. \]

1. Evaluate \(f( -1) ,\) \(f( 100) \), and \(f(200)\).
2. Graph \(f.\)
3. Find the domain, range, and the \(x\)- and \(y\)-intercepts of \(f.\)

Solution (a) \(f( -1) =0;\) \(f( 100) =10;\) \(f( 200) =0.2( 200) -10=30\)

(b) The graph of \(f\) consists of three pieces corresponding to each equation in the definition. The graph is the horizontal line \(y= 0\) on the interval \(( -\infty ,0) ,\) the horizontal line \(y=10\) on the interval \([ 0,100] \), and the line \(y=0.2x-10\) on the interval \(( 100,\infty ) \), as shown in Figure 11.

(c) \(f\) is a piecewise-defined function. Look at the values that \( x\) can take on: \(x<0,\) \(0\leq x\leq 100,\) \(x>100.\) We conclude the domain of \(f\) is all real numbers. The range of \(f\) is the number \(0\) and all real numbers greater than or equal to \(10.\) The \(x\)-intercepts are all the numbers in the interval \(( -\infty ,0) \); the \(y\)-intercept is \( 10 \).