Analyzing the Graph of a Polynomial Function

For the polynomial function \(f ( x ) =x^{2} ( x-4 ) ( x+1 ) \):

1. Find the \(x\)- and \(y\)-intercepts of the graph of \(f\).
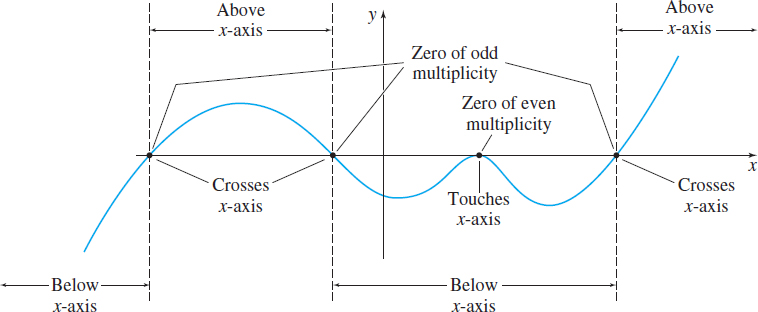
2. Determine whether the graph crosses or touches the \(x\)-axis at each \(x\)-intercept.
3. Plot at least one point to the left and right of each \(x\)-intercept and connect the points to obtain the graph.

19

Solution

1. The \(y\)-intercept is \(f ( 0 ) =0.\) The \(x\)-intercepts are the zeros of the function: \(0\), \(4\), and \(-1\).
2. \(0\) is a zero of multiplicity \(2\); the graph of \(f\) will touch the \(x\)-axis at \(0\). The numbers \(4\) and \(-1\) are zeros of multiplicity \(1\); the graph of \(f\) will cross the \(x\)-axis at \(4\) and \(-1\).
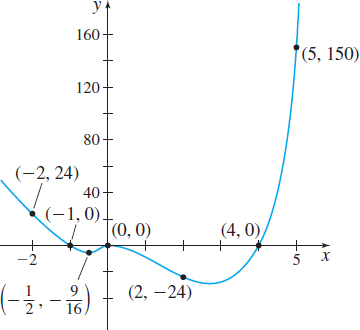
3. Since \(f ( -2 ) =24\), \(f \!\left( -\dfrac{1}{2} \right) =-\dfrac{9}{16}\), \(f ( 2 ) =-24\), and \(f ( 5 ) =150,\) the points \( ( -2,24 )\), \(\left( -\dfrac{1}{2},-\dfrac{9}{16} \right) \), \( ( 2,-24 )\), and \( ( 5,150 ) \) are on the graph. See Figure 31.