Determining Whether a Function Is One-to-One
Determine whether each of these functions is one-to-one:
- \(f(x) = x^{2}\)
- \(g(x) = x^{3}\)
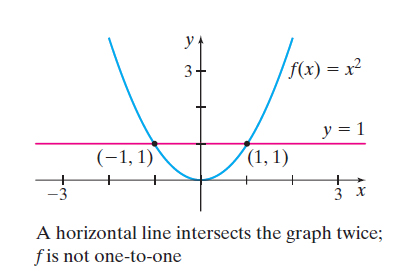
Solution (a) Figure 49 illustrates the Horizontal-line Test for the graph of \(f(x) = x^{2}\). The horizontal line \(y = 1\) intersects the graph of \(f\) twice, at \((1, 1)\) and at \((-1, 1)\), so \(f\) is not one-to-one.
(b) Figure 50 illustrates the horizontal-line test for the graph of \(g(x) = x^{3}\). Because every horizontal line intersects the graph of \(g\) exactly once, it follows that \(g\) is one-to-one.
