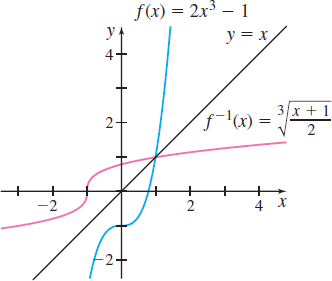
Finding the Inverse Function

The function \(f(x) = 2x^{3}-1\) is one-to-one. Find its inverse.

Solution We follow the steps given above.

Step 1  Write \(f\) as \(y = 2x^{3}-1\).

Step 2  Interchange the variables \(x\) and \(y\). \[ \ x = 2y^{3}-1 \]

This equation defines \(f^{-1}\) implicitly.

Step 3 Solve the implicit form of the inverse function for \(y\). \begin{eqnarray*} x+1 &=&2y^{3} \\[5pt] y^{3} &=&\dfrac{x+1}{2} \\[5pt] y &=&\sqrt[3]{\dfrac{x+1}{2}}=f^{-1}( x) \end{eqnarray*}

Step 4  Check the result. \[ \begin{array}{c} \;\;\;\;\;\;\;\;\;\;f^{ - 1} (f(x)) = f^{ - 1} (2x^3 - 1) = \sqrt[3]{{\frac{{(2x^3 - 1) + 1}}{2}}} = \sqrt[3]{{\frac{{2x^3 }}{2}}} = \sqrt[3]{{x^3 }} = x \\ f(f^{ - 1} (x)) = f\left( {\sqrt[3]{{\frac{{x + 1}}{2}}}} \right) = 2\left( {\sqrt[3]{{\frac{{x + 1}}{2}}}} \right)^3 - 1 = 2\left( {\frac{{x + 1}}{2}} \right) - 1 \\ \;\;\;\;\;\;\;\;\;= x + 1 - 1 = x \\ \end{array} \]