Using Properties (3), (4), and (5) of Logarithms

(a) \( \begin{array}{@{}rcll@{\quad}lcl} \log _{a} \big( x\displaystyle\sqrt{x^{2}+1} \big) &=&\log _{a}x+\log _{a}\displaystyle\sqrt{x^{2}+1} & & {\color{#0066A7}{\log _{a} ({uv})}}{\color{#0066A7}{=}}\,{\color{#0066A7}{\log _{a}u+\log_av}} \\[3pt] &=&\log _{a}x+\log _{a}( x^{2}+1) ^{1/2} & & \\[2pt] &=&\log _{a}x+\dfrac{1}{2}\log _{a}( x^{2}+1) & & {\color{#0066A7}{\log_{a}{u}^{r}}}{\color{#0066A7}{=}}\,{\color{#0066A7}{r\log _{a}u}} \end{array} \)

A-11

(b)

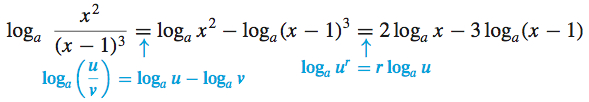
(c) \( \begin{array}[t]{lll} \log _{a}x+\log _{a}9+\log _{a}( x^{2}+1) -\log _{a}5 & =\log _{a} (9x) +\log _{a}( x^{2}+1) -\log _{a}5 & \\[5pt] & =\log _{a} [ 9x( x^{2}+1)] -\log _{a}5 & \\[5pt] & =\log _{a}\!\left[ \dfrac{9x( x^{2}+1) }{5}\right] \end{array} \)