Figure

Solving Inequalities Involving Absolute Value

Solve each inequality and graph the solution:

(a) \(\vert 3-4x\vert < 11\)

(b) \(\vert 2x+4\vert -1\leq 9\)

(c) \( \left\vert \dfrac{4x+1}{2}-\dfrac{3}{5}\right\vert >1\)

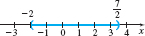
Solution (a) The absolute value is less than the number \(11,\) so statement (1) applies. \[ \begin{array}{@{{-4.5pc}}rcccc@{\quad}l} \vert 3-4x\vert &<&{11} & \\[3pt] -11 &<&3-4x&<&11&{\color{#0066A7}{\hbox{Apply statement (1).}}} \\[3pt] -14 &<&-4x&<&8 & {\color{#0066A7}{\hbox{Subtract 3 from each part.}}} \\[3pt] \dfrac{-14}{-4} &>&x&>&\dfrac{8}{-4} & {\color{#0066A7}{\raise5pt\hbox{Divide each part by \(-4\), which}}} \\[-9pt] &&&&&{\color{#0066A7}{\raise9pt\hbox{reverses the inequality signs.}}}\\[-5pt] -2 &<&x&<&\dfrac{7}{2} & {\color{#0066A7}{\hbox{Simplify and rearrange the ordering.}}} \end{array} \]

Multiplying (or dividing) an inequality by a negative quantity reverses the direction of the inequality sign.

The solutions are all the numbers in the open interval \(\!\left( -2,\dfrac{7}{2}\right)\!\). See Figure 4 for the graph of the solution.

Figure 4 \(-2<x<\dfrac{7}{2}\)

(b) We begin by putting \(\vert 2x+4\vert -1\leq 9\) into the form \(\vert u\vert \leq a\). \[ \begin{array}{@{{-4.7pc}}rclll@{\quad}l} \vert 2x+4\vert -1 &\leq &9 &\\[3pt] \vert 2x+4\vert &\leq &10 &&& {\color{#0066A7}{\hbox{Add 1 to each side.}}} \\[3pt] -10 &\leq &2x+4&\leq& 10 & {\color{#0066A7}{\hbox{Apply statement (1), but use \(\leq\).}}} \\[3pt] -14 &\leq &{2x}&\leq& 6 \\[3pt] -7 &\leq &{x}&\leq& 3 \end{array} \]

Figure 5 \(-7\leq x \leq 3\)

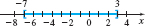
The solutions are all the numbers in the closed interval \([-7, 3]\) . See Figure 5 for the graph of the solution.

(c) \(\left\vert \dfrac{4x+1}{2}-\dfrac{3}{5}\right\vert > 1\) is in the form of statement (2). We begin by simplifying the expression inside the absolute value. \[ \left\vert \dfrac{4x+1}{2}-\dfrac{3}{5}\right\vert =\left\vert \dfrac{ 5( 4x+1) }{10}-\dfrac{2( 3) }{10}\right\vert =\left\vert \dfrac{20x+5-6}{10}\right\vert =\left\vert \dfrac{20x-1}{10} \right\vert \]

A-8

The original inequality is equivalent to the inequality below. \[ \left\vert \dfrac{20x-1}{10}\right\vert >1 \] \[ \begin{array}{@{{-2pc}}rcl@{\qquad}c@{\qquad}r@{\qquad}l} \dfrac{20x-1}{10} &<&-1 &\hbox{ or }& \dfrac{20x-1}{10}>1\hphantom{0} & {\color{#0066A7}{\hbox{Apply statement (2).}}} \\[8pt] 20x-1 &<&-10&\hbox{ or } &20x-1>10 \\[3pt] 20x &<&-9 &\hbox{ or }& 20x>11 \\[3pt] x\, &<&-\dfrac{9}{20} &\hbox{ or } & x>\dfrac{11}{20}\!\! \end{array} \]

Figure 6 \(x<-\dfrac{9}{20}\) or \(x>\dfrac{11}{20}\)

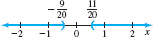
The solutions are all the numbers in the set \(\left( -\infty ,-\dfrac{9}{20}\right) \cup \left(\dfrac{11}{20},\infty \right) .\) See Figure 6 for the graph of the solution.