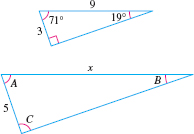
Using Similar Triangles

Given that the triangles in Figure 19 are similar, find the missing length \( x\) and angles \(A\), \(B\), and \(C\).

Solution Because the triangles are similar, corresponding angles have the same measure. So, \(A=71\mathbf{ {{}^\circ}}\), \(B=19\mathbf{ {{}^\circ}}\), and \(C=90\mathbf{ {{}^\circ}}\). Also corresponding sides are proportional. That is, \(\dfrac{3}{5}=\dfrac{ 9}{x}.\) We solve this equation for \(x\). \[ \begin{array}{r@{ }c@{ }l@{}l@{}l} \dfrac{3}{5} &=& \dfrac{9}{x} & & \\ 5x\cdot \dfrac{3}{5} &=& 5x\cdot \dfrac{9}{x} & & {\color{#0066A7}{\hbox{Multiply both sides by \(5x\).}}} \\ 3x&=&45 & & {\color{#0066A7}{\hbox{Simplify.}}} \\[0pt] x&=&15 & & {\color{#0066A7}{\hbox{Divide both sides by 3.}}} \end{array} \] The missing length is \(15\) units.