Graphing a Circle Whose Equation Is in General Form

Graph the equation \[ x^{2}+y^{2}+4x-6y+12=0 \]

Solution  We complete the square in both \(x\) and \(y\) to put the equation in standard form. First, we group the terms involving \(x\), group the terms involving \(y,\) and put the constant on the right side of the equation. The result is \[ ( x^{2}+4x) + ( y^{2}-6y) =-12 \]

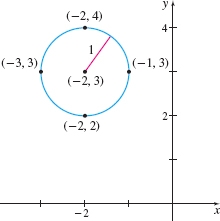
Next, we complete the square of each expression in parentheses. Remember that any number added to the left side of an equation must be added to the right side. \begin{eqnarray*} {( x^{2}+4x\underset{\underset{\color{#0066A7}{\hbox{Add \(\left( \dfrac{4}{2}\right) ^{\!\!\!2}=\, 4\)}}}{\color{#0066A7}{\displaystyle\uparrow}}}{+}4) + ( y^{2}-6y\underset{\underset{\color{#0066A7}{\hbox{Add \(\left( \dfrac{-6}{2}\right) ^{\!\!\!2}=\, 9\)}}} {\color{#0066A7}{\displaystyle \uparrow}}}{+}9) }&=&-12+4+9=1\\ ( x+2)^{2}+( y-3) ^{2}&=&1 {16pt}\quad {\color{#0066A7}{\hbox{Factor.}}} \end{eqnarray*}

This is the standard form of the equation of a circle with radius \(1\) and center at the point \(( -2,3)\). To graph the circle, we plot the center \(( -2,3)\) and points \(1\) unit to the right, to the left, above and below the point \(( -2,3)\), as shown in Figure 36.