Graph the equation: $9x^{2}+4y^{2}=36$

Solution  To put the equation in standard form, we divide each side by $36$. $$\dfrac{x^{2}}{4}+\dfrac{y^{2}}{9}=1$$

The graph of this equation is an ellipse. Since the larger number is under $y^{2}$, the major axis is along the $y$-axis. The center is at the origin (0, 0). It is easiest to graph an ellipse by finding its intercepts: $$\begin{array}{rcl@{\qquad\qquad\qquad\qquad}rcl} {x\hbox{-intercepts: Let }y=0} & {y\hbox{-intercepts: Let }x=0} \\[5pt] \dfrac{x^{2}}{4}+\dfrac{0^{2}}{9} &=& 1 & 0^{2}+\dfrac{y^{2}}{9}&=&1 \\[9pt] x^{2}&=&4 & y^{2}&=&9 \\[5pt] {x=-2 \hbox{ and } x=2} & {y=-3 \hbox{ and } y=3} \end{array}$$

A-24

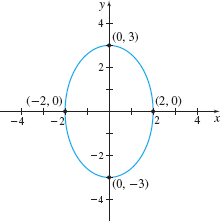
Figure 40 $9x^2 + 4y^2 = 36$

The points $( -2,0)$, $( 2,0)$, $( 0,-3)$ , $( 0,3)$ are the intercepts of the ellipse. See Figure 40.