Graph the equation $\dfrac{y^{2}}{4}-\dfrac{x^{2}}{5}=1$.

Solution  The graph of $\dfrac{y^{2}}{4}-\dfrac{x^{2}}{5}=1$ is a hyperbola. The hyperbola consists of two branches, one opening up, the other opening down, like the graph in Figure 41(b). The hyperbola has no $x$ -intercepts. To find the $y$-intercepts, we let $x=0$ and solve for $y.$ $$\begin{array}{l} \dfrac{y^{2}}{4}=1 \\[11pt] y^{2}=4 \\[5pt] y=-2\qquad\hbox{ or} \qquad y=2 \end{array}$$

A-25

The $y$-intercepts are $-2$ and $2$, so the vertices are $(0,-2)$ and ($0,2$). The transverse axis is the vertical line $x=0.$ To graph the hyperbola, let $y=\pm\, 3$ (or any numbers $\geq$$2$ or $\leq$$-2$). Then $$\begin{array}{rclll} \dfrac{y^{2}}{4}-\dfrac{x^{2}}{5}&=&1 & & \\ \dfrac{9}{4}-\dfrac{x^{2}}{5}&=&1 & & {\color{#0066A7}{y=\pm\, 3}} \\ ~\ \ \ \ \ \ \dfrac{x^{2}}{5}&=&\dfrac{5}{4} & & \\ ~\ \ \ \ \ \ \ x^{2}&=&\dfrac{25}{4} & & \\ x=-\dfrac{5}{2} &\hbox{or}& x=\dfrac{5}{2} \\ \end{array}$$

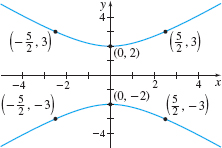
Figure 42 $\dfrac{y^{2}}{4}-\dfrac{x^{2}}{5}=1$

The points $\left( -\dfrac{5}{2},3\right)$, $\left( -\dfrac{5}{2},-3\right)$, $\left( \dfrac{5}{2},3\right)$, and $\left( \dfrac{5}{2},-3\right)$ are on the hyperbola. See Figure 42 for the graph.