Find the slope $m$ and the $y$-intercept of the equation $2x+4y=8$. Graph the equation.

Solution  To obtain the slope and $y$-intercept, we write the equation in slope-intercept form by solving for $y$. $$\begin{eqnarray*} 2x+4y &=&8 \\[3pt] 4y &=&-2x+8 \\[3pt] y &=&-\dfrac{1}{2}x+2 \quad{\color{#0066A7}{y=mx+b}} \end{eqnarray*}$$

A-20

The coefficient of $x$ is the slope. The slope is $-\dfrac{1}{2}.$ The constant $2$ is the $y$-intercept, so the point $( 0,2)$ is on the graph. Now use the slope $-\dfrac{1}{2}.$ Starting at the point $( 0,2)$, we move $2$ units to the right and then $1$ unit down to the point $(2, 1)$. We plot this point and draw a line through the two points. See Figure 29.

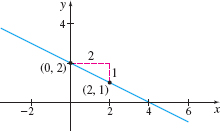
Figure 29 $2x+4y=8$

When two lines in the plane do not intersect, they are parallel.