Graph the equation $( x+3) ^{2}+( y-2) ^{2}=16$.

Solution  This is the standard form of an equation of a circle. To graph the circle, we first identify the center and the radius of the circle. $$\begin{eqnarray*} ( x+3) ^{2}+( y-2) ^{2}&=&16\\[0pt] ( x-( \underset{\underset{\color{#0066A7}{h}}{\color{#0066A7}{\uparrow}}}{-3}))^{2} +( y-\underset{\underset{\color{#0066A7}{k}}{\color{#0066A7}{\uparrow}}}{2})^{2}&=&\underset{\underset{\color{#0066A7}{r^2}}{\color{#0066A7}{\uparrow}}}{4^{2}}\\[0pt] \end{eqnarray*}$$

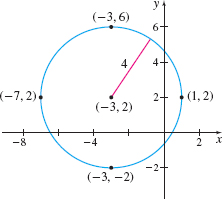
Figure 35 $( x+3) ^{2}+( y-2) ^{2}=16$

The circle has its center at the point$( -3, 2) ;$ its radius is $4$ units. To graph the circle, we plot the center $( -3, 2) .$ Then we locate the four points on the circle that are $4$ units to the left, to the right, above, and below the center. These four points are used as guides to obtain the graph. See Figure 35.