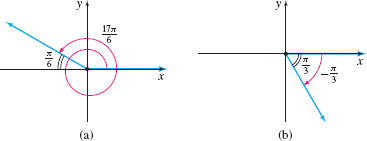
Using Reference Angles

Find the exact value of: (a) \(\cos \dfrac{17\pi }{6}\)

(b) \(\tan\left( -\dfrac{\pi }{3}\right) \)

Solution  (a) Refer to Figure 58(a) on page A-31. The angle \(\dfrac{17\pi }{6}\) is in quadrant II, where the cosine function is negative. The reference angle for \(\dfrac{17\pi }{6}\) is \(\dfrac{\pi }{6}.\) Since \(\cos \dfrac{\pi }{6}=\dfrac{\displaystyle\sqrt{3}}{2}\), \[ \cos \dfrac{17\pi }{6}=-\cos \dfrac{\pi }{6}=-\dfrac{\displaystyle\sqrt{3}}{2} \]

(b) Refer to Figure 58(b). The angle \(-\dfrac{\pi }{3}\) is in quadrant IV, where the tangent function is negative. The reference angle for \(-\dfrac{\pi }{3}\) is \(\dfrac{\pi }{3}.\) Since \(\tan \dfrac{\pi }{3}=\displaystyle\sqrt{3}\), \[ \tan \left( -\dfrac{\pi }{3}\right) =-\tan \dfrac{\pi }{3}=-\displaystyle\sqrt{3} \]

A-31