Find any asymptotes of the rational function $R(x)=\dfrac{3x^{2}-12}{ 2x^{2}-9x+10}$.

Solution We begin by factoring $R.$ $$\begin{equation*} R(x)=\dfrac{3x^{2}-12}{2x^{2}-9x+10}=\dfrac{3(x-2)(x+2)}{(2x-5)(x-2)} \end{equation*}$$

The domain of $R$ is $\left\{ x |\ x\neq \dfrac{5}{2}\hbox{ and }x\neq 2\right\}$. Since $R$ is a rational function, it is continuous on its domain, that is, all real numbers except $x=\dfrac{5}{2}$ and $x=2$.

To check for vertical asymptotes, we find the limits as $x$ approaches $\dfrac{5}{2}$ and $2$. First we consider $\lim\limits_{x\rightarrow \frac{ 5}{2}^{-}}R(x)$. $$\begin{equation*} \lim\limits_{x\rightarrow \frac{5}{2}^{-}}R(x)=\!\!\lim\limits_{x\rightarrow \frac{5}{2}^{-}}\left[ \frac{3(x-2)(x+2)}{(2x-5)(x-2)}\right] =\!\!\lim\limits_{x\rightarrow \frac{5}{2}^{-}}\left[ \frac{3(x+2)}{(2x-5)} \right] =3\!\!\lim\limits_{x\rightarrow \frac{5}{2}^{-}}\frac{x+2}{2x-5}=-\infty \end{equation*}$$

That is, as $x$ approaches $\dfrac{5}{2}$ from the left, $R$ becomes unbounded in the negative direction.

The graph of $R$ has a vertical asymptote at $x=\dfrac{5}{2}$.

To determine the behavior to the right of $x=\dfrac{5}{2}$, we find the right-hand limit. $$\begin{equation*} \lim\limits_{x\rightarrow \frac{5}{2}^{+}}R(x)=\lim\limits_{x\rightarrow \frac{5}{2}^{+}}\left[ \frac{3(x+2)}{(2x-5)}\right] = 3\lim\limits_{x\rightarrow \frac{5}{2}^{+}}\frac{x+2}{2x-5}=\infty \end{equation*}$$

As $x$ approaches $\dfrac{5}{2}$ from the right, the graph of $R$ becomes unbounded in the positive direction.

Next we consider $\lim\limits_{x\rightarrow 2}R(x)$. $$\begin{equation*} \lim\limits_{x\rightarrow 2}R(x)=\lim\limits_{x\rightarrow 2}\frac{ 3(x-2)(x+2)}{(2x-5)(x-2)}=\lim\limits_{x\rightarrow 2}\frac{3(x+2)}{2x-5}= \frac{3(2+2)}{2\cdot 2-5}=\frac{12}{-1}=-12 \end{equation*}$$

The function $R$ does not have a vertical asymptote at $2.$

Since $2$ is not in the domain of $R,$ the graph of $R$ has a hole at the point $(2,-12)$.

Figure 63 $R(x) = \dfrac{3x^2-12}{2x^2-9x+10}$

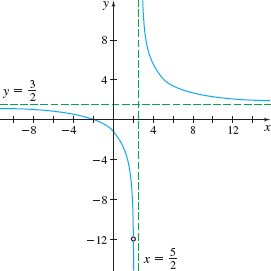
To check for horizontal asymptotes, we find the limits at infinity. $$\begin{eqnarray*} \lim_{x\rightarrow \infty }R( x) &=&\lim_{x\rightarrow \infty } \frac{3x^{2}-12}{2x^{2}-9x+10}\underset{\underset{\underset{\color{#0066A7}{\hbox{and denominator by \(2x^{2}\)}}}{\color{#0066A7}{\hbox{Divide the numerator}}}}{\color{#0066A7}{\uparrow}}} {=} \lim_{x\rightarrow \infty }\frac{\dfrac{3}{2}-\dfrac{6}{x^{2}}}{1-\dfrac{9}{ 2x}+\dfrac{5}{x^{2}}}=\frac{\lim\limits_{x\rightarrow \infty }\left( \dfrac{3 }{2}-\dfrac{6}{x^{2}}\right) }{\lim\limits_{x\rightarrow \infty }\left( 1- \dfrac{9}{2x}+\dfrac{5}{x^{2}}\right) }\\ &=&\dfrac{\dfrac{3}{2}-0}{1-0+0}=\frac{3 }{2} \\ \end{eqnarray*}$$

127

$$\begin{eqnarray*} \lim_{x\rightarrow \infty }R( x) &=&\lim_{x\rightarrow \infty } \frac{3x^{2}-12}{2x^{2}-9x+10}\underset{\underset{\underset{\color{#0066A7}{\hbox{and denominator by \(2x^{2}\)}}}{\color{#0066A7}{\hbox{Divide the numerator}}}}{\color{#0066A7}{\uparrow}}} {=} \lim_{x\rightarrow \infty }\frac{\dfrac{3}{2}-\dfrac{6}{x^{2}}}{1-\dfrac{9}{ 2x}+\dfrac{5}{x^{2}}}\\ &=&\frac{\lim\limits_{x\rightarrow \infty }\left( \dfrac{3 }{2}-\dfrac{6}{x^{2}}\right) }{\lim\limits_{x\rightarrow \infty }\left( 1- \dfrac{9}{2x}+\dfrac{5}{x^{2}}\right) }=\frac{3 }{2} \end{eqnarray*}$$

The line $y=\dfrac{3}{2}$ is a horizontal asymptote of the graph of $R$ for $x$ unbounded in the negative direction and for $x$ unbounded in the positive direction.