Finding a Vertical Asymptote

Find any vertical asymptote(s) of the graph of \(f(x)=\dfrac{x}{(x-3)^{2}}\).

Solution The domain of \(f\) is \(\{x|x\neq 3\}\). Since \(3\) is the only number for which the denominator of \(f\) equals zero, we construct Table 13 and investigate the one-sided limits of \(f\) as \(x\) approaches \(3\). Table 13 suggests that \[ \lim\limits_{x\rightarrow 3}\dfrac{x}{(x-3)^{2}}=\infty \]

So, \(x=3\) is a vertical asymptote of the graph of \(f\).

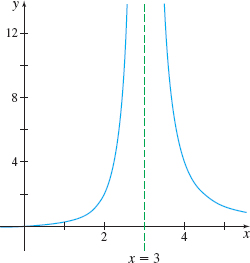
Figure 52 \(f(x)=\dfrac{x}{(x-3)^2}\)
TABLE 13
\(\underrightarrow{x~\hbox{approaches 3 from the left}}\) \(\underleftarrow{x~\hbox{approaches 3 from the right}}\)
\(x\) \(2.9\) \(2.99\) \(2.999\) \(\ \rightarrow \) 3 \(\leftarrow\) \(3.001\) \(3.01\) \(3.1\)
\(f( x) =\dfrac{x}{(x-3)^{2}}\) \(290\) \(29{,}900\) \(2{,}999{,}000\) \(f(x)\) becomes unbounded \(3{,}001{,}000\) \(30{,}100\) \(310\)

120

Figure 52 shows the graph of \(f( x) =\dfrac{x}{( x-3)^{2}}\) and its vertical asymptote.