Finding a Limit at Infinity

Find \(\lim\limits_{x\rightarrow \infty }\dfrac{5x^{4}-3x^{2}}{2x^{2}+1}\).

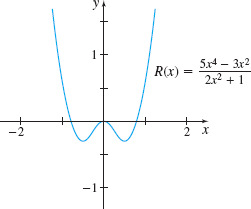
Solution \(R( x) =\dfrac{5x^{4}-3x^{2}}{2x^{2}+1}\) is a rational function defined for all real numbers. Find the limit by dividing each term of the numerator and the denominator by the term with the highest power of \(x\) that appears in the denominator, in this case, \(2x^{2}\). Then \[ \begin{eqnarray*} \lim\limits_{x\rightarrow \infty }\dfrac{5x^{4}-3x^{2}}{2x^{2}+1} \underset{\underset{\underset{\color{#0066A7}{\hbox{and denominator by \(2x^{2}\)}}}{\color{#0066A7}{\hbox{Divide the numerator}}}}{\color{#0066A7}{\uparrow}}}{=}\lim\limits_{x\rightarrow \infty }\dfrac{ \dfrac{5x^{4}-3x^{2}}{2x^{2}}}{\dfrac{2x^{2}+1}{2x^{2}}}=\lim\limits_{x \rightarrow \infty }\dfrac{\dfrac{5x^{2}}{2}-\dfrac{3}{2}}{1+\dfrac{1}{2x^{2} }}=\infty \end{eqnarray*} \]

because \(\dfrac{5x^{2}}{2}-\dfrac{3}{2}\) \(\rightarrow \infty \) and \(1+\dfrac{ 1}{2x^{2}}\) \(\rightarrow \) \(1\) as \(x\rightarrow \infty \).