Find the horizontal asymptotes, if any, of $f(x)=\dfrac{3x-2}{4x-1}.$

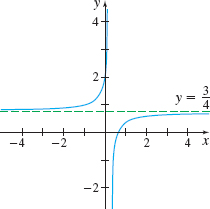
Figure 62 $f(x) = \dfrac{3x-2}{4x-1}$

Solution We examine the two limits at infinity: $\lim\limits_{x\rightarrow -\infty }\dfrac{3x-2}{4x-1}$ and $\lim\limits_{x\rightarrow \infty }\dfrac{3x-2}{4x-1}.$

Since $\lim\limits_{x\rightarrow -\infty }\dfrac{3x-2}{4x-1}=\dfrac{3}{4},$ the line $y=\dfrac{3}{4}$ is a horizontal asymptote of the graph of $f$ for $x$ unbounded in the negative direction.

Since $\lim\limits_{x\rightarrow \infty }\dfrac{3x-2}{4x-1}=\dfrac{3}{4},$ the line $y=\dfrac{3}{4}$ is a horizontal asymptote of the graph of $f$ for $x$ unbounded in the positive direction.