Using the \(\epsilon \)-\(\delta \) Definition of a Limit

Prove: \(\lim\limits_{x\rightarrow 2}x^{2}=4\).

Solution Given any \(\epsilon >0\), we must show there is a number \(\delta >0\) so that \begin{equation*} \hbox{whenever }\quad 0 \lt \vert x-2\vert \lt \delta \qquad \hbox{ then } \vert x^{2}-4\vert \lt \epsilon \end{equation*}

To establish a connection between \(\vert x^{2}-4\vert \) and \( \vert x-2\vert \), we write \(\left\vert x^{2}-4\right\vert \) as \begin{equation*} \left\vert x^{2}-4\right\vert =\left\vert \,(x+2)(x-2)\right\vert =\left\vert x+2\right\vert \cdot \vert x-2\vert \end{equation*}

Now, if we can find a number \(K\) for which \(\left\vert x+2\right\vert \lt K\), then we can choose \(\delta =\dfrac{\epsilon }{K}\). To find \(K\), we restrict \( x\) to some interval centered at \(2\). For example, suppose the distance between \(x\) and \(2\) is less than \(1\). Then \begin{equation*} \begin{array}{rcl@{\qquad}l} \\[-5pc] &&\vert x-2\vert \lt 1 & \\[3pt] -1&\lt&x-2 \lt 1 & \\[3pt] 1&\lt&x \lt 3 & {\color{#0066A7}{\hbox{Simplify.}}} \\ 1+2&\lt&x+2 \lt 3+2 & {\color{#0066A7}{\hbox{Add 2 to each part. }}} \\ 3&\lt&x+2 \lt 5 & \end{array} \end{equation*}

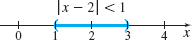
134

In particular, we have \(\vert x+2\vert \lt 5\). It follows that whenever \(\vert x-2\vert \lt 1\), \begin{equation*} \vert x^{2}-4\vert =\left\vert x+2\right\vert \cdot \vert x-2\vert \lt 5\,\vert x-2\vert \hbox{ } \end{equation*}

If \(\vert x-2\vert \lt \delta =\dfrac{\epsilon }{5}\), then \( \left\vert \hbox{ }x^{2}-4\right\vert \lt 5\,\vert x-2\vert \lt 5\cdot \dfrac{\epsilon }{5}=\epsilon \), as desired.

But before choosing \(\delta =\dfrac{\epsilon }{5}\), we must remember that there are two constraints on \(\vert x-2\vert \). Namely, \begin{equation*} \vert x-2\vert \lt 1\qquad \hbox{and}\qquad \vert x-2\vert \lt \dfrac{\epsilon }{5} \end{equation*}

To ensure that both inequalities are satisfied, we select \(\delta \) to be the smaller of the numbers 1 and \(\dfrac{\epsilon }{5}\), abbreviated as \( \delta =\min \left\{ 1,\dfrac{\epsilon }{5}\right\} \). Now, \[ \hbox{whenever } \vert x-2\vert \lt \delta =\min \left\{ 1,\dfrac{\epsilon }{5}\right\} \hbox{ then } \vert x^{2}-4\vert \lt \epsilon \]

proving \(\lim\limits_{x\rightarrow 2}x^{2}=4\).