Use a graph to investigate $\lim\limits_{x\rightarrow 0}f(x)$ if $f( x) =\left\{ \begin{array}{l@{\qquad}l} x & \hbox{if }\quad x<0 \\ 1 & \hbox{if }\quad x>0 \end{array} \right. .$

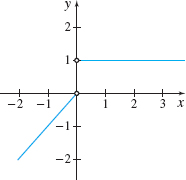
Figure 13 $f( x) =\left\{ \begin{array}{l@{\qquad}l} x & \hbox{if }\quad x<0 \\ 1 & \hbox{if }\quad x>0 \end{array} \right.$

Solution Figure 13 shows the graph of $f$. We first investigate the one-sided limits. The graph suggests that, as $x$ approaches 0 from the left, $$\begin{equation*} \lim_{x\rightarrow 0^{-}}f(x)=0 \end{equation*}$$

and as $x$ approaches 0 from the right, $$\begin{equation*} \lim_{x\rightarrow 0^{+}}f(x)=1 \end{equation*}$$

Since there is no single number that the values of $f$ approach when $x$ is close to 0, we conclude that $\lim\limits_{x\rightarrow 0}f(x)$ does not exist.