Using the Intermediate Value Theorem to Approximate a Real Zero of a Function

The function \(f(x)=x^{3}+x^{2}-x-2\) has a zero in the interval \((1,2)\). Use the Intermediate Value Theorem to approximate the zero correct to three decimal places.

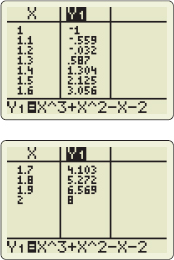
Solution Using the TABLE feature on a graphing utility, we subdivide the interval \([1,2]\) into \(10\) subintervals, each of length \(0.1\). Then we find the subinterval whose endpoints have opposite signs, or the endpoint whose value equals \(0\) (in which case, the exact zero is found). From Figure 34, since \(f ( 1.2) =-0.032\) and \(f (1.3) =0.587\), by the Intermediate Value Theorem, a zero lies in the interval \(( 1.2,1.3)\). Correct to one decimal place, the zero is \(1.2\).

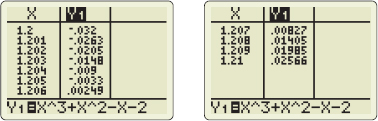
Repeat the process by subdividing the interval \([ 1.2,1.3]\) into \(10\) subintervals, each of length \(0.01.\) See Figure 35. We conclude that the zero is in the interval \((1.20, 1.21)\), so correct to two decimal places, the zero is \(1.20\).

Now subdivide the interval \(\left[ 1.20,1.21\right]\) into \(10\) subintervals, each of length \(0.001.\) See Figure 36.

We conclude that the zero of the function \(f\) is \(1.205,\) correct to three decimal places.