Determine if $f(x)=\dfrac{\sqrt{x^{2}+2}}{x^{2}-4}$ is continuous at the numbers $-2$, $0$, and $2$.

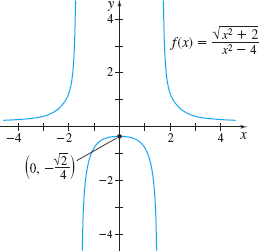
Figure 23 $f$ is continuous at 0; $f$ is discontinuous at $-2$ and $2$.

Solution The domain of $f$ is $\{x|x\neq -2$, $x\neq 2\}$. Since $f$ is not defined at $-2$ and $2$, the function $f$ is not continuous at $-2$ and at $2$. The number $0$ is in the domain of $f$. That is, $f$ is defined at $0$, and $f(0)=-\dfrac{\sqrt{2}}{4}$. Also, $$\begin{eqnarray*} \lim_{x\rightarrow 0}f(x)&=&\lim_{x\rightarrow 0}\frac{\sqrt{x^{2}+2}}{ x^{2}-4}=\frac{\lim\limits_{x\rightarrow 0}\sqrt{x^{2}+2}}{ \lim\limits_{x\rightarrow 0}(x^{2}-4)}=\frac{\sqrt{\lim\limits_{x\rightarrow 0}(x^{2}+2)}}{\lim\limits_{x\rightarrow 0}x^{2}-\lim\limits_{x\rightarrow 0}4 }\\[5pt] &=&\frac{\sqrt{0+2}}{0-4}=-\frac{\sqrt{2}}{4}=f(0) \end{eqnarray*}$$

The three conditions of continuity at a number are met. So, the function $f$ is continuous at $0$.

Figure 23 shows the graph of $f$.